题目内容
12.在锐角△ABC中,AB=26cm,AC=25cm,BC边上的高为24cm,则△ABC的面积为204cm2.分析 分两种情况:①∠B为锐角;②∠B为钝角;利用勾股定理求出BD、CD,即可求出BC的长.
解答 解:在Rt△ABD中,
BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=10,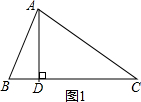
在Rt△ADC中,
CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=7,
∴BC=BD+CD=17,
∴△ABC的面积为$\frac{1}{2}$×24×17=204;
故答案为:204.
点评 本题主要考查了勾股定理;熟练掌握勾股定理,画出图形是解答此题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
3.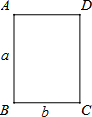 如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
 如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )| A. | V甲>V乙,S甲=S乙 | B. | V甲<V乙,S甲=S乙 | C. | V甲=V乙,S甲=S乙 | D. | V甲>V乙,S甲<S乙 |
4.有一个三位数,现将它最左边的数字移至最右边所得到的数比原来的数小144;而由它的十位数字与个位数字所组成的两位数除以百位数字,商是7,余数是4.如果设这个三位数的百位为x,十位与个位数字组成的两位数为y,可得方程组是( )
| A. | $\left\{\begin{array}{l}{(100x+y)-(100y+x)=144}\\{y=7x+4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{(100x+y)-(10y+x)=144}\\{y=7x+4}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{(10y+x)-(100x+y)=144}\\{y=7x+4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{(100x+y)-(10x+y)=144}\\{y=7x+4}\end{array}\right.$ |
1.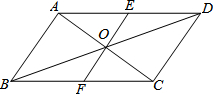 如图,平行四边形ABCD中,EF过对角线的交点O,AB=3,AD=4,OF=1.3,则四边形ABEF的周长为( )
如图,平行四边形ABCD中,EF过对角线的交点O,AB=3,AD=4,OF=1.3,则四边形ABEF的周长为( )
 如图,平行四边形ABCD中,EF过对角线的交点O,AB=3,AD=4,OF=1.3,则四边形ABEF的周长为( )
如图,平行四边形ABCD中,EF过对角线的交点O,AB=3,AD=4,OF=1.3,则四边形ABEF的周长为( )| A. | 8.3 | B. | 9.6 | C. | 12.6 | D. | 13.6 |
 如图,AB是⊙O的直径,C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为4.
如图,AB是⊙O的直径,C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为4.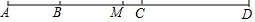 已知,如图B,C两点把线段AD分成2:4:3三部分,M是AD的中点,CD=6cm,则线段AD的长为多少厘米?
已知,如图B,C两点把线段AD分成2:4:3三部分,M是AD的中点,CD=6cm,则线段AD的长为多少厘米?