题目内容
11.若|x2-4x+3|=kx+3有且只有两个不相等的实数根,则k的取值范围是-3≤k<-1或k>-4-2$\sqrt{6}$.分析 首先画出y=|x2-4x+3|的图象,得出A(0,3),B(1,0),C(3,0).直线AB斜率为:k=-3,直线AC斜率为:k=-1.根据图形求解即可.
解答  解:根据题意画出图形,如图所示.
解:根据题意画出图形,如图所示.
则A(0,3),B(1,0),C(3,0).
易求直线AB斜率为:k=-3,直线AC斜率为:k=-1.
抛物线开口向下部分:y=-x2+4x-3,与直线y=kx+3相切时,得k=-4-2$\sqrt{6}$.
根据图形可知,若|x2-4x+3|=kx+3有且只有两个不相等的实数根,
-3≤k<-1或k>-4-2$\sqrt{6}$.
故答案为-3≤k<-1或k>-4-2$\sqrt{6}$.
点评 本题考查了根的判别式,二次函数的性质,利用数形结合是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
1.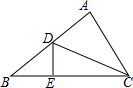 如图,在△ABC中,∠A=90°,点D是AB边上的一点,过D点作BC的垂线,垂足为点E,已知:AB=4cm,BC=8cm,CD=7cm,则△DBE的周长为( )
如图,在△ABC中,∠A=90°,点D是AB边上的一点,过D点作BC的垂线,垂足为点E,已知:AB=4cm,BC=8cm,CD=7cm,则△DBE的周长为( )
 如图,在△ABC中,∠A=90°,点D是AB边上的一点,过D点作BC的垂线,垂足为点E,已知:AB=4cm,BC=8cm,CD=7cm,则△DBE的周长为( )
如图,在△ABC中,∠A=90°,点D是AB边上的一点,过D点作BC的垂线,垂足为点E,已知:AB=4cm,BC=8cm,CD=7cm,则△DBE的周长为( )| A. | 5cm | B. | 6cm | C. | $\frac{9+3\sqrt{3}}{2}$cm | D. | 8cm |
19.抛物线y=(m+1)x2+2mx+3上有两点A(-3,y1)、B(5,y2)、C点(x0,y0)为此抛物线顶点,且y1>y2≥y0,则m的取值范围为( )
| A. | m>-1 | B. | m<-$\frac{1}{2}$ | C. | $-\frac{1}{2}$<m<1 | D. | -1<m<-$\frac{1}{2}$ |
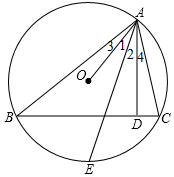 △ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).
△ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).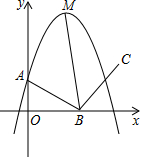 如图,抛物线y=-2x2+4x+1交y轴点A,顶点是M,点B是x轴上的一个动点,连结AB,BM,将线段AB绕点B顺时针旋转90°到BC的位置,当BM平分∠ABC时,点B的坐标是(1,0)或(2,0).
如图,抛物线y=-2x2+4x+1交y轴点A,顶点是M,点B是x轴上的一个动点,连结AB,BM,将线段AB绕点B顺时针旋转90°到BC的位置,当BM平分∠ABC时,点B的坐标是(1,0)或(2,0).