题目内容
5.数轴上A,B两点表示的数分别是$\sqrt{2}$和3$\sqrt{3}$,则A,B两点间表示的整数的点共有4个.分析 首先分别估算出$\sqrt{2}$和3$\sqrt{3}$的大小,然后根据数轴的特征,判断出A,B两点间表示的整数的点共有多少个即可.
解答 解:∵$\sqrt{2}$≈1.414,3$\sqrt{3}$≈3×1.732=5.196,
∴A,B两点间表示的整数的点共有4个:2、3、4、5.
故答案为:4.
点评 (1)此题主要考查了实数与数轴问题,要熟练掌握,解答此题的关键是要明确:实数与数轴上的点是一一对应关系.任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.数轴上的任一点表示的数,不是有理数,就是无理数.
(2)此题还考查了估算无理数的大小的方法,要熟练掌握.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
13.如果正比例函数y=(k-5)x的图象在第二、四象限内,则k的取值范围是( )
| A. | k<0 | B. | k>0 | C. | k>5 | D. | k<5 |
20.已知关于x的不等式$\left\{\begin{array}{l}{x-a≤0}\\{7+2x>1}\end{array}\right.$的整数解共有5个,则a的取值范围是( )
| A. | 2≤a<3 | B. | 2<a<3 | C. | -3<a<-2 | D. | -3≤a<2 |
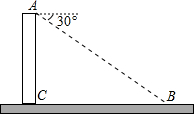 如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为10$\sqrt{3}$m(结果保留根号).
如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为10$\sqrt{3}$m(结果保留根号).