题目内容
15.化简:$\sqrt{2+\sqrt{3}}$.分析 被开方数变形后,利用二次根式的性质化简,即可得到结果.
解答 解:$\sqrt{2+\sqrt{3}}$=$\sqrt{\frac{4+2\sqrt{3}}{2}}$=$\sqrt{\frac{(\sqrt{3}+1)^{2}}{2}}$=$\frac{\sqrt{2}}{2}×(\sqrt{3}+1)$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
点评 此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.下列图形,既是轴对称图形,又是中心对称图形的是( )
| A. | 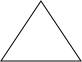 | B. | 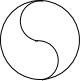 | C. |  | D. | 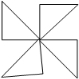 |
7.在Rt△ABC中,∠B=90°,AB=8,BC=6,将△ABC沿MN折叠(M、N分别在AC、AB上,且不与端点重合),使点A与BC上的点D重合,点D把线段BC分成长度之比是1:2的两条线段,则线段BN的长为( )
| A. | $\frac{15}{8}$ | B. | 3 | C. | 3或$\frac{15}{4}$ | D. | $\frac{15}{4}$或4 |
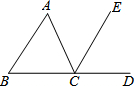 写出图中∠B的一个同位角∠ECD或∠ACD.
写出图中∠B的一个同位角∠ECD或∠ACD.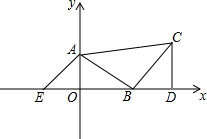 在直角坐标系中,△ABC是等腰直角三角形,∠ABC=90°,点A(0,3),点B(4,0),CD⊥x轴,垂足为D.
在直角坐标系中,△ABC是等腰直角三角形,∠ABC=90°,点A(0,3),点B(4,0),CD⊥x轴,垂足为D.