题目内容
10.解方程组:$\left\{\begin{array}{l}{2({x}^{2}+3y)+{x}^{2}-3y=15(1)}\\{{x}^{2}+3y-4({x}^{2}-3y)=3(2)}\end{array}\right.$.分析 把x2-3y和x2+3y各自看做一个整体,(1)-(2)×2消去x2+3y,求出x2-3y的值,代入(2)求出x2+3y的值,组成方程组,解方程组得到答案.
解答 解:(1)-(2)×2得:
9(x2-3y)=9,
∴x2-3y=1③,
把③代入(2)解得x2+3y=7,
∴$\left\{\begin{array}{l}{{x}^{2}+3y=7}\\{{x}^{2}-3y=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=1}\end{array}\right.$.
点评 本题考查的是二元二次方程组的解法,掌握加减消元法解方程组是解题的关键.

练习册系列答案
相关题目
18.解方程组$\left\{\begin{array}{l}{3x-2y=1}\\{3x+y=3}\end{array}\right.$加减消元法消元后,正确的方程为( )
| A. | 6x-y=4 | B. | 3y=2 | C. | -3y=2 | D. | -y=2 |
2.下列实数中,属于无理数的是( )
| A. | $\sqrt{4}$ | B. | $\root{3}{9}$ | C. | 3.14 | D. | $\frac{1}{3}$ |
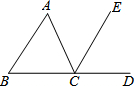 写出图中∠B的一个同位角∠ECD或∠ACD.
写出图中∠B的一个同位角∠ECD或∠ACD.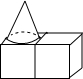 如图,由两个相同的小正方体和一个圆锥组成的几何体,其左视图是( )
如图,由两个相同的小正方体和一个圆锥组成的几何体,其左视图是( )