题目内容
14.已知关于x的不等式组$\left\{\begin{array}{l}{2x+4>0}\\{3x-k<6}\end{array}\right.$.(1)当k为何值时,该不等式组的解集为-2<x<1;
(2)若该不等式组只有3个正整数解,求一个满足条件的整数k的值.
分析 (1)求出不等式组的解集,根据已知得出$\frac{6+k}{3}$=1,从而求出k的值.
(2)首先解不等式组确定不等式组的解集,然后根据不等式组只有3个正整数解即可得到一个关于k的不等式组,求得k的范围.
解答 解:(1)解不等式组$\left\{\begin{array}{l}{2x+4>0}\\{3x-k<6}\end{array}\right.$可得解集为-2<x<$\frac{6+k}{3}$,
∵不等式组的解集为-2<x<1,
∴$\frac{6+k}{3}$=1,
解得k=-3.
(2)解不等式组$\left\{\begin{array}{l}{2x+4>0}\\{3x-k<6}\end{array}\right.$可得解集为-2<x<$\frac{6+k}{3}$,
不等式组有3个正整数解,则正整数解是:1,2,3.
则3<$\frac{6+k}{3}$≤4.
解得:3<k≤6.
点评 本题考查了不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
2.下列实数中,属于无理数的是( )
| A. | $\sqrt{4}$ | B. | $\root{3}{9}$ | C. | 3.14 | D. | $\frac{1}{3}$ |
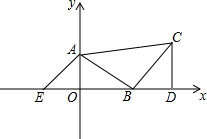 在直角坐标系中,△ABC是等腰直角三角形,∠ABC=90°,点A(0,3),点B(4,0),CD⊥x轴,垂足为D.
在直角坐标系中,△ABC是等腰直角三角形,∠ABC=90°,点A(0,3),点B(4,0),CD⊥x轴,垂足为D.