题目内容
8.下列四种说法:(1)当x<2时,分式$\frac{(x+1)^{2}}{x-2}$的值恒为负数;
(2)分式$\frac{3}{8-y}$的值可以等于零;
(3)方程x2-$\frac{1}{x+1}$=1-$\frac{1}{x+1}$的解是x=±1
(4)将分式$\frac{2xy}{x+y}$中的x、y的都扩大为原来的3倍,分式的值也扩大为原来的3倍.
其中正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1)方式的除法法则,分子和分母同号时,分式的为正,分子和分母异号时,分式的为负,注意等号;
(2)利用分式的值要为零时分子等于零,分母不等于0,即可;
(3)分式方程的解必须要检验;
(4)用分式的性质判定即可‘
解答 解:(1)∵x<2,
∴x-2<0,
∵(x+1)2≥0,
∴$\frac{(x+1)^{2}}{x-2}$≤0;
故(1)错;
(2)∵$\frac{3}{8-y}$的分子是3,不等于0,
∴分式$\frac{3}{8-y}$的值不可能是0;
故(2)错;
(3)∵x2-$\frac{1}{x+1}$=1-$\frac{1}{x+1}$,
∴x=±1,
当x=1时,x+1≠0,
∴x=1是原方程的解,
当x=-1时,x+1=0,
∴x=-1是曾根,
故(3)错;
(4)∴分式$\frac{2xy}{x+y}$中的x、y的都扩大为原来的3倍,
∴$\frac{2×3x×3y}{3x+3y}$=$\frac{6xy}{x+y}$=3×$\frac{2xy}{x+y}$,
故(4)正确;
故选A
点评 此题是分式的基本性质,主要考查了分式的基本性质,分式的值,分式方程的解,解本题的关键是分式的基本要掌握好.

练习册系列答案
相关题目
18.下列图案中,属于轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.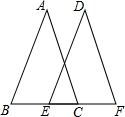 如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )
如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )
 如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )
如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.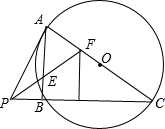 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )| A. | 10 | B. | 12 | C. | $5\sqrt{5}$ | D. | $5\sqrt{6}$ |
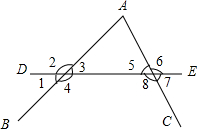 如图,直线DE截AB,AC,构成八个角:
如图,直线DE截AB,AC,构成八个角: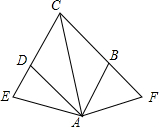 如图,点E.F分别是菱形ABCD的边CD与CB延长线上的点,且DE=BF,求证:∠E=∠F.
如图,点E.F分别是菱形ABCD的边CD与CB延长线上的点,且DE=BF,求证:∠E=∠F.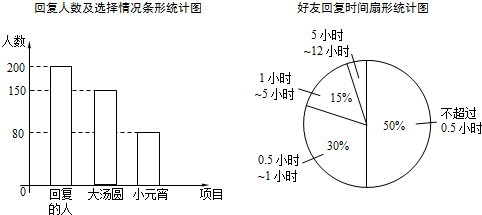
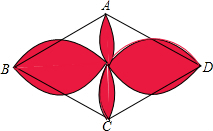 如图,四边形ABCD是菱形,AB=10cm,∠ABC=60°,分别以ABCD的四条边为直径作半圆.求图中红色部分的面积.
如图,四边形ABCD是菱形,AB=10cm,∠ABC=60°,分别以ABCD的四条边为直径作半圆.求图中红色部分的面积.