题目内容
16. 如图,直线l1在平面直角坐标系中与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线l1上.
如图,直线l1在平面直角坐标系中与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线l1上.(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
分析 (1)根据平移的法则即可得出点C的坐标,设直线l1的解析式为y=kx+c,根据点B、C的坐标利用待定系数法即可求出直线l1的解析式;
(2)由点B的坐标利用待定系数法即可求出直线l2的解析式,再根据一次函数图象上点的坐标特征求出点A、E,根据三角形的面积公式即可求出△ABE的面积.
解答 解:(1)由平移法则得:C点坐标为(-3+1,3-2),即(-2,1).
设直线l1的解析式为y=kx+c,
则$\left\{\begin{array}{l}{3=-3k+c}\\{1=-2k+c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{c=-3}\end{array}\right.$,
∴直线l1的解析式为y=-2x-3.
(2)把B点坐标代入y=x+b得,
3=-3+b,解得:b=6,
∴y=x+6.
当x=0时,y=6,
∴点E的坐标为(0,6).
当x=0时,y=-3,
∴点A坐标为(0,-3),
∴AE=6+3=9,
∴△ABE的面积为$\frac{1}{2}$×9×|-3|=$\frac{27}{2}$.
点评 本题考查了待定系数法求一次函数解析式、坐标与图形变化中的平移以及三角形的面积,根据点的坐标利用待定系数法求出函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列命题错误的是( )
| A. | 等弧对等弦 | |
| B. | 三角形一定有外接圆和内切圆 | |
| C. | 平分弦的直径垂直于弦 | |
| D. | 经过切点且垂直于切线的直线必经过圆心 |
8.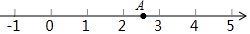 如图所示的数轴上,
如图所示的数轴上,
(1)A点表示数为2.5.
(2)已知点B表示$\frac{7}{4}$,点C表示2$\frac{2}{3}$;在数轴上分别画出点B、C,并将A、B、C所表示的数用“<”连接起来.
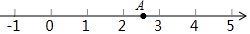 如图所示的数轴上,
如图所示的数轴上,(1)A点表示数为2.5.
(2)已知点B表示$\frac{7}{4}$,点C表示2$\frac{2}{3}$;在数轴上分别画出点B、C,并将A、B、C所表示的数用“<”连接起来.
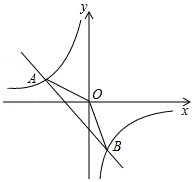 如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.
如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.