题目内容
11.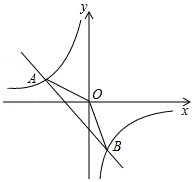 如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.
如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.(1)试确定上述一次函数和反比例函数的表达式;
(2)求△AOB的面积.
分析 (1)由点B的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数的解析式,再将点A的坐标代入其内求出n值,由点A、B的坐标利用待定系数法即可求出一次函数的解析式;
(2)设一次函数图象与y轴交于点C,根据一次函数图象上点的坐标特征找出点C的坐标,再利用三角形的面积公式即可求出△AOB的面积.
解答 解:(1)∵一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点,
∴将B(1,-3)代入反比例函数y2=$\frac{m}{x}$,
得:-3=$\frac{m}{1}$,解得:m=-3,
∴反比例函数为y2=-$\frac{3}{x}$.
将A(-2,n)代入反比例函数y2=-$\frac{3}{x}$,
得:n=$\frac{3}{2}$,即A(-2,$\frac{3}{2}$),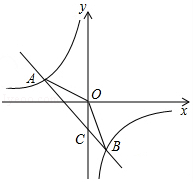
将A(-2,$\frac{3}{2}$)、B(1,-3)代入一次函数y1=kx+b,
得:$\left\{\begin{array}{l}{-3=k+b}\\{\frac{3}{2}=-2k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=-\frac{3}{2}}\end{array}\right.$,
∴一次函数为y1=-$\frac{3}{2}$x-$\frac{3}{2}$.
(2)如图,设一次函数图象与y轴交于点C,
当x=0时,y=-$\frac{3}{2}$,
∴C(0,-$\frac{3}{2}$),
∴S△AOB=S△AOC+S△COB=$\frac{1}{2}$×$\frac{3}{2}$×[1-(-2)]=$\frac{1}{2}$×$\frac{3}{2}$×3=$\frac{9}{4}$.
点评 本题考查了一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及反比例函数图象上点的坐标特征,根据点的坐标利用待定系数法求出函数解析式是解题的关键.

| A. | 5 | B. | 10 | C. | 25 | D. | ±10 |
| A. | (1,2) | B. | (-1,-2) | C. | (1,-2) | D. | (2,-1) |
| 日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 单位:万人 | +1.4 | +0.8 | +0.4 | -0.6 | -0.2 | +0.2 | -1.6 |
(1)10月2日的游客人数是3.2万人.
(2)这七天内游客人数最多的是3日,游客数为3.6万人.
(3)请计算这七天总共有多少游客去麦积山风景区?
 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论
如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论 如图,直线l1在平面直角坐标系中与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线l1上.
如图,直线l1在平面直角坐标系中与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线l1上.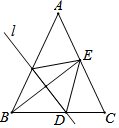 如图,在△ABC中,AB=AC=12$\sqrt{5}$,BC=24,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.
如图,在△ABC中,AB=AC=12$\sqrt{5}$,BC=24,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.