题目内容
 如图,在高度是24米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=
如图,在高度是24米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=考点:解直角三角形的应用-仰角俯角问题
专题:
分析:作AE⊥CD于点E,则△AED和△ABD都是等腰直角三角形,即可求得DE的长,然后在直角三角形中利用三角函数求得CE的长,进而求得CD的长.
解答: 解:作AE⊥CD于点E.
解:作AE⊥CD于点E.
在直角△ABD中,∠ADB=45°,
∴DE=AE=BD=AB=24(米),
在直角△AEC中,CE=AE•tan∠CAE=24×
=8
(米).
则CD=(24+8
)米.
故答案为:(24+8
).
 解:作AE⊥CD于点E.
解:作AE⊥CD于点E.在直角△ABD中,∠ADB=45°,
∴DE=AE=BD=AB=24(米),
在直角△AEC中,CE=AE•tan∠CAE=24×
| ||
| 3 |
| 3 |
则CD=(24+8
| 3 |
故答案为:(24+8
| 3 |
点评:本题考查解直角三角形的应用-仰角俯角问题的应用,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
2014年3月份,萧山市区一周空气质量报告中某项污染指数的数据是:61,75,61,63,50,63,61,则下列表述错误的是( )
| A、中位数是62 |
| B、众数是61 |
| C、平均数是62 |
| D、极差是25 |
 如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.
如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.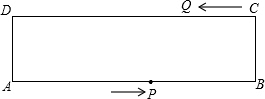 如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过
如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过 如图,在△ABC中,AB=AC=7,BC=2,点Q是BC的延长线上一点,且AQ=BQ+CQ,求tanQ=
如图,在△ABC中,AB=AC=7,BC=2,点Q是BC的延长线上一点,且AQ=BQ+CQ,求tanQ=