题目内容
 如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.
如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.(1)求船P到海岸线MN的距离(结果保留根号);
(2)若船A﹑船B分别以30海里/时﹑20海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)过点P作PC⊥AB于点C,在Rt△BPC中解出PE即可;
(2)在Rt△PAC中,求出PA,分别计算出两艘船需要的时间,即可作出判断.
(2)在Rt△PAC中,求出PA,分别计算出两艘船需要的时间,即可作出判断.
解答: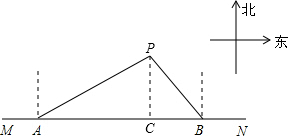 解:(1)过点P作PC⊥AB于点C.
解:(1)过点P作PC⊥AB于点C.
由已知得:∠PAC=90°-60°=30°,∠PBC=90°-30°=60°,
∴PC=PBsin∠PBC=30×sin60゜=30×
=15
(海里).
答:船P到海岸线MN的距离为15
海里;
(2)在Rt△PAC中,∵∠PAC=30°,
∴PA=2PC=30
(海里),
∴船A到达船P处用时为:30
÷30=
(小时),
船B到达船P处用时为:30÷20=1.5(小时),
∵
>1.5,
∴船B先到达船P处.
 解:(1)过点P作PC⊥AB于点C.
解:(1)过点P作PC⊥AB于点C.由已知得:∠PAC=90°-60°=30°,∠PBC=90°-30°=60°,
∴PC=PBsin∠PBC=30×sin60゜=30×
| ||
| 2 |
| 3 |
答:船P到海岸线MN的距离为15
| 3 |
(2)在Rt△PAC中,∵∠PAC=30°,
∴PA=2PC=30
| 3 |
∴船A到达船P处用时为:30
| 3 |
| 3 |
船B到达船P处用时为:30÷20=1.5(小时),
∵
| 3 |
∴船B先到达船P处.
点评:本题考查了解直角三角形的应用,解答本题的关键是理解方向角的定义,能利用三角函数值计算有关线段,难度一般.

练习册系列答案
相关题目
 已知点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,求证:△AOD≌△BOC.
已知点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,求证:△AOD≌△BOC.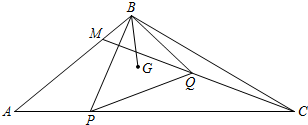
 如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.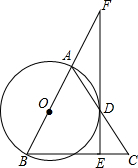 如图,在△ABC中,AB=BC,以AB为直径的⊙0与AC于点D,作DE⊥BC垂足为E,延长ED交BA的延长线于点F.
如图,在△ABC中,AB=BC,以AB为直径的⊙0与AC于点D,作DE⊥BC垂足为E,延长ED交BA的延长线于点F. 函数y=kx+b的大致图象如图所示,则当x<0时,y的取值范围是
函数y=kx+b的大致图象如图所示,则当x<0时,y的取值范围是 如图,在高度是24米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=
如图,在高度是24米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=