题目内容
若某直角三角形的一个锐角的正切值为
，则这个直角三角形中另一个锐角的余弦值为 ．
| 1 |
| 3 |
考点：互余两角三角函数的关系
专题：
分析：根据题意，画出图形，设两直角边为x，3x，根据勾股定理可以计算结果．
解答：解：如图所示，设BC=x，则，AC=3x，∠A的正切值为
，所以AB=
x，
∴cosB=
=
=
故答案为：
．
| 1 |
| 3 |
| 10 |
∴cosB=
| BC |
| AB |
| x | ||
|
| ||
| 10 |
故答案为：
| ||
| 10 |
点评：本题主要考查了三角函数的求值运算，设参法是解决这类问题常用的方法．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，在高度是24米的小山A处测得建筑物CD顶部C处的仰角为30°，底部D处的俯角为45°，则这个建筑物的高度CD=
如图，由边长为1的小正方形组成的网格中，正方形ABGH，BCFG，CDEF的顶点都在网格的格点上．则tan∠BHD=
小明同学将直角三角形直角顶点置于平面直角坐标系的原点O，两直角边与抛物线y=-某人帐户现存款a元，每月支出b元，收入c元（a、b、c都是常数且大于0），则帐户余额（不计利息）与月份的函数图象可能是下图中的（ ）
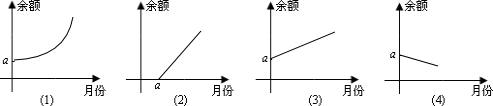
| A、（1）（3） |
| B、（3）（4） |
| C、（1）（3）（4） |
| D、（2）（3）（4） |
已知整数x满足是不等式组
，则x的算术平方根为（ ）
|
| A、2 | ||
| B、±2 | ||
C、
| ||
| D、4 |