题目内容
5.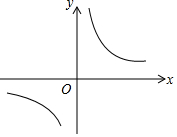 已知:Rt△ABC中,∠C=90°,∠B=60°,且BC=1,若把△ABC放入如图的直角坐标系中,使斜边AB在x轴,点C在双曲线y=$\frac{\sqrt{3}}{x}$上.
已知:Rt△ABC中,∠C=90°,∠B=60°,且BC=1,若把△ABC放入如图的直角坐标系中,使斜边AB在x轴,点C在双曲线y=$\frac{\sqrt{3}}{x}$上.(1)求△ABC斜边AB上的高CD;
(2)求点C的坐标;
(3)求点D的坐标;
(4)求点A的坐标.
分析 (1)先求△ABC的边长AC和AB的长,根据面积法求高CD的长;
(2)分两种情况:
①当点C在第一象限的反比例图象上时,如图1,由高得点C的纵坐标代入反比例函数的解析式可求得横坐标;
②当点C在第三象限的反比例图象上时,如图2,同理可求得点C的坐标;
(3)根据两个图形分别求出D的坐标;
(4)根据两个图形分别求出A的坐标.
解答 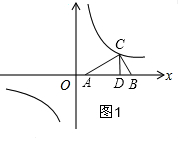 解:(1)在Rt△ABC中,∠B=60°,
解:(1)在Rt△ABC中,∠B=60°,
∴∠CAB=30°,
∴AB=2BC=2,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
$\sqrt{3}$×1=2CD,
CD=$\frac{\sqrt{3}}{2}$;
(2)分两种情况: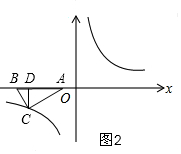
①当点C在第一象限的反比例图象上时,如图1,
∵CD=$\frac{\sqrt{3}}{2}$,
把y=$\frac{\sqrt{3}}{2}$代入y=$\frac{\sqrt{3}}{x}$中,x=2,
∴C(2,$\frac{\sqrt{3}}{2}$),
②当点C在第三象限的反比例图象上时,如图2,
此时点C的纵坐标为-$\frac{\sqrt{3}}{2}$,
把y=-$\frac{\sqrt{3}}{2}$代入到y=$\frac{\sqrt{3}}{x}$中,x=-2,
∴C(-2,-$\frac{\sqrt{3}}{2}$),
综上所述,点C的坐标为(2,$\frac{\sqrt{3}}{2}$)或(-2,-$\frac{\sqrt{3}}{2}$);
(3)如图1,点D的坐标为(2,0)
如图2,点D的坐标为(-2,0)
综上所述,点D的坐标为(2,0)或(-2,0);
(4)cos30°=$\frac{AD}{AC}$,
AD=$\frac{\sqrt{3}}{2}$×$\sqrt{3}$=$\frac{3}{2}$,
∴OA=OD-AD=2-$\frac{3}{2}$=$\frac{1}{2}$,
如图1,点A的坐标为($\frac{1}{2}$,0),
如图2,点A的坐标为(-$\frac{1}{2}$,0),
综上所述,点A的坐标为($\frac{1}{2}$,0)或(-$\frac{1}{2}$,0).
点评 本题考查了反比例函数图象上点的坐标的特征和含30°角的直角三角形的性质,掌握30°角所对的直角边是斜边的一半,本题还利用了面积法求直角三角形斜边上的高,这一方法在数学上应用比较广泛,要熟练掌握;本题采用了分类讨论的思想,因为已知中没有说明直角三角形放置的位置,所以要分两种情况进行讨论.

| A. | -2 | B. | 1 | C. | -1 | D. | 2 |
 如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )
如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
| A. | b-c | B. | b+c | C. | -b+c | D. | -b-c |
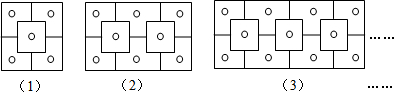
| A. | 23个 | B. | 24个 | C. | 25个 | D. | 26个 |
 已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.
已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.