题目内容
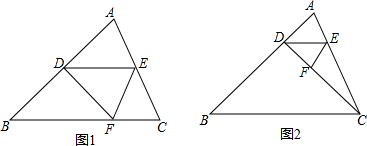
17.如图,△ABC中,∠B=45°,∠C=65°,点D在AB上,点E在AC上,且DE∥BC,△ADE沿DE折叠,点A对称点为F点.(1)若点A落在BC边上(如图1),求证:△BDF是等腰直角三角形;
(2)若点A落在三角形内(如图2),过点D、F、C在一条直线上,求△CEF各角的度数.
分析 (1)利用平行线的性质得出∠ADE=45°,再利用翻折变换的性质得出∠ADE=∠EDF=45°,进而得出∠BDF=90°即可得出答案;
(2)利用平行线的性质得出∠ADE=45°、∠AED=65°,由翻折可得∠FDE=∠ADE=45°、∠FED=∠AED=65°,进而有∠FEC=50°、∠FCE=∠ACB-∠BCD=20°,根据内角和定理可得∠EFC度数.
解答 解:(1)∵∠B=45°,DE∥BC,
∴∠ADE=45°,
∵△ADE沿DE折叠,点A对应点为F点,
∴∠ADE=∠EDF=45°,
∴∠BDF=90°,
∴△BDF是等腰直角三角形;
(2)∵DE∥BC,∠B=45°,∠ACB=65°,
∴∠ADE=∠B=45°,∠AED=∠ACB=65°,
∵△ADE沿DE折叠,点A对应点为F点,
∴∠FDE=∠ADE=45°,∠FED=∠AED=65°,
∴∠BCD=∠FDE=45°,∠FEC=180°-∠FED-∠AED=50°,
由∠ACB=65°,可得∠FCE=∠ACB-∠BCD=20°,
在△ECF中,∠EFC=180°-∠ECF-∠CEF=110°,
故△CEF中,∠FEC=50°,∠ECF=20°,∠EFC=110°.
点评 此题主要考查了翻折变换的性质以及平行线的性质和等腰直角三角形的判定以及三角形内角和定理等知识,正确利用翻折变换的性质得出∠ADE=∠EDF、∠FED=∠AED是解题关键.

练习册系列答案
相关题目
2.某班统计了10名同学在一周内的读书时间,他们一周内的读书时间累计如下表,则这10名同学在一周内累计时间的众数是( )
| 一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
| 人数(个) | 1 | 4 | 3 | 2 |
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
12.已知一次函数y=kx+b,k,b从-1,-2,3中随机取一个值,则该函数图象经过一、二、四象限的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{6}$ |
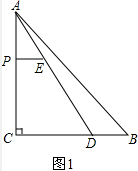 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,D是BC边上一点,CD=3cm,点P为边AC上一动点(点P与A、C不重合),过点P作PE∥BC,交AD于点E,点P以1cm/s的速度从A到C匀速运动.设点P的运动时间为t(s),DE的长为y(cm),求y关于t的函数关系式,并写出t的取值范围.
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,D是BC边上一点,CD=3cm,点P为边AC上一动点(点P与A、C不重合),过点P作PE∥BC,交AD于点E,点P以1cm/s的速度从A到C匀速运动.设点P的运动时间为t(s),DE的长为y(cm),求y关于t的函数关系式,并写出t的取值范围.