题目内容
6．已知x2-1=0，则式子x2+$\frac{1}{x^2}$的值是2．分析 根据x2-1=0，可得x2的值，从而可以得到x2+$\frac{1}{x^2}$的值．
解答 解：∵x2-1=0，
∴x2=1，
∴x2+$\frac{1}{x^2}$=1+$\frac{1}{1}$=1+1=2，
故答案为：2．
点评 本题考查分式的混合运算，解题的关键是根据已知条件找出所求问题需要的条件．
练习册系列答案
相关题目
16．如图1，在△ABC中，AB=AC，∠BAC=120°，点O是BC的中点，点D沿B→A→C方向从B运动到C．设点D经过的路径长为x，图1中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是图1中的（ ）
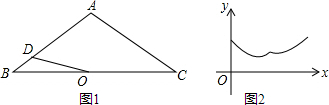
| A． | BD | B． | OD | C． | AD | D． | CD |
17．点（-3，2）向下平移3个单位长度，再向右平移4个单位长度后位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
如图，将一副三角板的直角顶点重合，摆放在桌面上，若∠BOC=63°，则∠AOD=117°．
1．$（\frac{2}{5}{）^{2015}}•（-\frac{5}{2}{）^{2016}}$的计算结果是（ ）
| A． | $\frac{2}{5}$ | B． | $-\frac{2}{5}$ | C． | $\frac{5}{2}$ | D． | $-\frac{5}{2}$ |
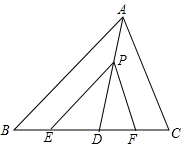如图，在△ABC中，点D，E，F在边BC上，点P在线段AD上，若PE∥AB，∠PFD=∠C，点D到PE和PF的距离相等．求证：点D到AB和AC的距离相等．