题目内容
15．有5张卡片，上面分别画有：圆、正方形、等边三角形、正五边形、线段，将卡片画面朝下随意放在桌上，任取一张，那么取到卡片对应图形是中心对称图形的概率是$\frac{3}{5}$．分析 先根据中心对称图形的定义判断圆、正方形、线段为中心对称图形，然后根据概率公式求解．
解答 解：共有5种可能的结果数，其中圆、正方形、线段为中心对称图形，所以取到卡片对应图形是中心对称图形的概率=$\frac{3}{5}$．
故答案为$\frac{3}{5}$．
点评 本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．也考查了中心对称图形．
练习册系列答案
相关题目
5．下列语句：
①两条不相交的直线叫做平行线；
②过直线外一点有且只有一条直线与已知直线垂直；
③若AB=BC，则点B是AC的中点；
④若两角的两边互相平行，则这两个角一定相等；
其中说法正确的个数是（ ）
①两条不相交的直线叫做平行线；
②过直线外一点有且只有一条直线与已知直线垂直；
③若AB=BC，则点B是AC的中点；
④若两角的两边互相平行，则这两个角一定相等；
其中说法正确的个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
3．下列变形错误的是（ ）
| A． | 如果x+7=26，那么x+5=24 | B． | 如果3x+2y=2x-y，那么3x+3y=2x | ||
| C． | 如果2a=5b，那么2ac=5bc | D． | 如果3x=4y，那么$\frac{3x}{{a}^{2}}$=$\frac{4y}{{a}^{2}}$ |
10．掷一枚六个面分别标有1，2，3，4，5，6的正方体骰子，则向上一面的数不大于4的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{4}$ |
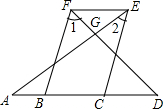如图，A、B、C、D四点在同一条直线上，∠AGD=90°，且∠1=∠D，∠2=∠A．求证：FB∥EC．
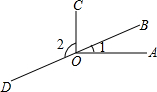如图，∠1=20°，∠AOC=90°，点B，O，D在同一直线上，则∠2=110°．