题目内容
8.已知a=$\frac{1}{2015}$+2014,b=$\frac{1}{2015}$+2015,c=$\frac{1}{2015}$+2016,则代数式2(a2+b2+c2-ab-bc-ca)=6.分析 根据a、b、c的值,分别求出a-b=-1,b-c=-1,c-a=2,c-b=1进而把代数式2(a2+b2+c2-ab-bc-ac)分组分解,即可得出答案.
解答 解:∵a=$\frac{1}{2015}$+2014,b=$\frac{1}{2015}$+2015,c=$\frac{1}{2015}$+2016,
∴a-b=-1,b-c=-1,c-a=2,c-b=1,
∴2(a2+b2+c2-ab-bc-ac),
=2[a(a-b)+b(b-c)+c(c-a)],
=2(-a-b+2c),
=2[(c-a)+(c-b)],
=2×3,
=6.
故答案为:6.
点评 此题主要考查了因式分解的应用,根据题意正确的分解因式得出(-a-b+2c)的值是解决问题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
18.下列事件是必然事件的是( )
| A. | 抛掷一枚硬币四次,有两次正面朝上 | |
| B. | 打开电视频道,正在播放《奔跑吧,兄弟》 | |
| C. | 射击运动员射击一次,命中十环 | |
| D. | 方程x2-2x-1=0必有实数根 |
3.下列变形,是因式分解的是( )
| A. | x2-2xy+y2-16=(x-y+4)(x-y-4) | B. | x2+3x-16=(x-2)(x+5)-6 | ||
| C. | (x+4)(x-4)=x2-16 | D. | ${x^2}+1=x({x+\frac{1}{x}})$ |
 如图,把一块直角三角板的直角顶点放在直角尺的一边上,如果∠1=34°,那么∠2的度数是56°.
如图,把一块直角三角板的直角顶点放在直角尺的一边上,如果∠1=34°,那么∠2的度数是56°.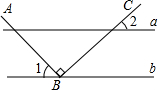 如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,则∠2的度数为35°.
如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,则∠2的度数为35°.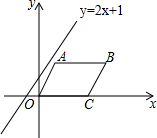 在平面直角坐标系中,?OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过6秒该直线可将□OABC的面积平分.
在平面直角坐标系中,?OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过6秒该直线可将□OABC的面积平分.