题目内容
13.计算:(1)$\frac{a-b}{a}$÷$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$
(2)$\frac{{a}^{2}}{a-1}$-a-1.
分析 (1)先把分子分母因式分解,再把除法运算化为乘法运算,然后合并即可;
(2)先进行通分得到原式=$\frac{{a}^{2}}{a-1}$-$\frac{(a+1)(a-1)}{a-1}$,然后进行同分母的减法运算即可.
解答 解:(1)原式=$\frac{a-b}{a}$•$\frac{a(a-b)}{(a+b)(a-b)}$
=$\frac{a-b}{a+b}$;
(2)原式=$\frac{{a}^{2}}{a-1}$-$\frac{(a+1)(a-1)}{a-1}$
=$\frac{{a}^{2}-{a}^{2}+1}{a-1}$
=$\frac{1}{a-1}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.

练习册系列答案
相关题目
3.-5的相反数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | -5 |
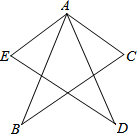 如图,AB=AD,AC=AE,∠CAD=∠EAB.求证:BC=DE.
如图,AB=AD,AC=AE,∠CAD=∠EAB.求证:BC=DE. 如图,已知蚂蚁以均匀的速度沿台阶由A爬行到E,那么蚂蚁爬行的高度h随时间t变化的图象是( )
如图,已知蚂蚁以均匀的速度沿台阶由A爬行到E,那么蚂蚁爬行的高度h随时间t变化的图象是( )



 现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( ) 已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F. 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为28cm2,则△BEF的面积=7cm2.
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为28cm2,则△BEF的面积=7cm2.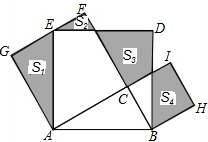 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4等于( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4等于( )