题目内容
10.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,试判断分别满足下列条件时,△ABC是否为直角三角形,并说明理由.(1)a:b:c=1:2:3;
(2)a=7,b=24,c=25;
(3)a=2.5,b=2,c=3.
分析 (1)根据三边的比值可设a=x,b=2x,c=3x,利用勾股定理的逆定理判断即可;
(2)根据勾股定理的逆定理判断即可;
(3)根据勾股定理的逆定理判断即可.
解答 解:(1)∵a:b:c=1:2:3,
∴可设a=x,b=2x,c=3x,
∵a2+b2=5x2≠c2,
∴△ABC不是直角三角形;
(2)∵a=7,b=24,c=25,
∴a2+b2=c2,
∴△ABC是直角三角形;
(3)∵a=2.5,b=2,c=3,
∴a2+b2≠c2,
∴△ABC不是直角三角形.
点评 本题考查了直角三角形的判定,注意在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图,已知△ABC,∠ACB=90°,点D、E在AB上,AD=DE=EB,CD2+CE2=1,求AB的长.
如图,已知△ABC,∠ACB=90°,点D、E在AB上,AD=DE=EB,CD2+CE2=1,求AB的长.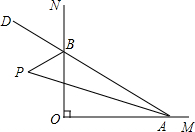 如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么?
如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么? 如图,在等腰直角三角形ABC中,AD是斜边BC上的高,则AD=BD=CD,请说明理由.
如图,在等腰直角三角形ABC中,AD是斜边BC上的高,则AD=BD=CD,请说明理由.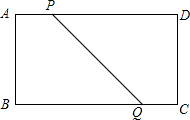 如图,四边形ABCD是矩形,AD=16cm,AB=8cm,动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,点Q以2cm/s的速度向B移动
如图,四边形ABCD是矩形,AD=16cm,AB=8cm,动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,点Q以2cm/s的速度向B移动