题目内容
20.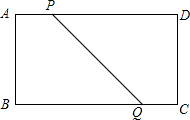 如图,四边形ABCD是矩形,AD=16cm,AB=8cm,动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,点Q以2cm/s的速度向B移动
如图,四边形ABCD是矩形,AD=16cm,AB=8cm,动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,点Q以2cm/s的速度向B移动(1)P、Q两点从出发开始几秒后,四边形ABQP的面积是矩形面积的$\frac{3}{5}$?
(2)P、Q从开始出发几秒后,PQ=4$\sqrt{13}$cm?
分析 (1)由题中数据可先求出矩形的面积,设x秒后,四边形ABQP的面积是矩形面积的$\frac{3}{5}$,根据梯形面积公式列出方程,求解即可;
(2)设出发y秒后PQ=4$\sqrt{13}$cm,作PE⊥BC于E,在直角△PEQ中,由勾股定理得出方程82+(16-3y-2y)2=(4$\sqrt{13}$)2,解方程即可.
解答 解:(1)矩形ABCD的面积S=16×8=128cm2,
$\frac{3}{5}$S矩形=$\frac{3}{5}$×128=76.8cm2,
设x秒后,四边形ABQP的面积是矩形面积的$\frac{3}{5}$,
即$\frac{1}{2}$(3x+16-2x)×8=76.8,
解得x=3.2.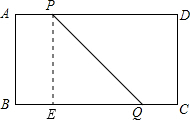 即P、Q两点从出发开始3.2秒后,四边形ABQP的面积是矩形面积的$\frac{3}{5}$.
即P、Q两点从出发开始3.2秒后,四边形ABQP的面积是矩形面积的$\frac{3}{5}$.
(2)设出发y秒后PQ=4$\sqrt{13}$cm,作PE⊥BC于E,则BE=AP=3y,EQ=BC-BE-CQ=16-3y-2y.
在直角△PEQ中,由勾股定理可得:82+(16-3y-2y)2=(4$\sqrt{13}$)2,
解得y=0.8或5.6.
即P、Q从开始出发0.8或5.6秒后,PQ=4$\sqrt{13}$cm.
点评 本题主要考查了一元二次方程的应用,矩形的性质以及勾股定理的运用,掌握梯形的面积公式,准确作出辅助线利用勾股定理是解题的关键.

练习册系列答案
相关题目
10.如果关于x的二次方程a(1+x2)+2bx=c(1-x2)有两个相等的实数根,那么以正数a,b,c为边长的三角形是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 任意三角形 |
 已知:如图△ABC中,CD是∠ACB平分线,DE∥BC,AD:DB=2:3,AC=a,求DE的长.
已知:如图△ABC中,CD是∠ACB平分线,DE∥BC,AD:DB=2:3,AC=a,求DE的长.