题目内容
1.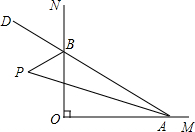 如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么?
如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么?
分析 根据三角形的一个外角等于和它不相邻的两个内角的和,∠OBD=∠OAB+∠MON,∠PBD=∠APB+∠PAB,再根据角平分线的定义∠BAP=$\frac{1}{2}$∠OAB,∠PBD=$\frac{1}{2}$∠OBD,代入整理即可得到∠P=$\frac{1}{2}$∠MON=45°.
解答 解:∠P的大小不会发生变化,
理由:∵AP平分∠OAB,
∴∠BAP=$\frac{1}{2}$∠OAB,
∵BP平分∠OBD,
∴∠PBD=$\frac{1}{2}$∠OBD,
∵∠OBD=∠MON+∠OAB,∠PBD=∠APB+∠BAP,
∴∠P=∠PBD-∠BAP=$\frac{1}{2}$(∠MON+∠OAB)-$\frac{1}{2}$∠OAB=$\frac{1}{2}$∠MON=$\frac{1}{2}$×90°=45°.
点评 本题考查的是三角形内角和定理,角平分线的性质,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
 如图,A城气象台测得一热带风暴中心O从A城正西方向300km处向东北方向移动,距风暴中心200km的范围内为受影响区域,问:A城是否会受到这次热带风暴的影响?请说明理由.
如图,A城气象台测得一热带风暴中心O从A城正西方向300km处向东北方向移动,距风暴中心200km的范围内为受影响区域,问:A城是否会受到这次热带风暴的影响?请说明理由.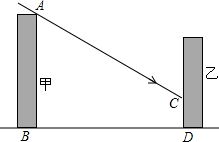 如图,在我国北方某居民区有一座甲楼,坐落在正南正北方向,楼高16米,要在甲楼的北面建一座乙楼,已知冬至这一天正午时太阳光线与水平线的夹角是32°.
如图,在我国北方某居民区有一座甲楼,坐落在正南正北方向,楼高16米,要在甲楼的北面建一座乙楼,已知冬至这一天正午时太阳光线与水平线的夹角是32°.