题目内容
9.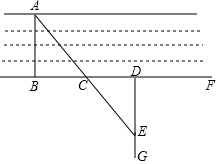 小明家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C、D使CD=CB,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段DE的长度就是AB的长.
小明家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C、D使CD=CB,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段DE的长度就是AB的长.(1)按小明的想法填写题目中的空格;
(2)请完成推理过程.
分析 (1)根据全等三角形的性质进行填空,构造全等三角形即可;
(2)首先证明△ABC≌△EDC,进而可根据全等三角形对应边相等可得DE=AB.
解答 解:(1)在与AB垂直的岸边BF上取两点C、D使CD=CB,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段 DE的长度就是AB的长.
故答案为:CB; 一条直线; DE;
(2)由题意得,∵DG⊥BF,
∴∠CDE=90°
在△ABC和△EDC中$\left\{\begin{array}{l}{∠ABC=∠EDC=90°}\\{CB=DC}\\{∠ACB=∠ECD}\end{array}\right.$,
∴△ABC≌△EDC(ASA)
∴DE=AB(全等三角形的对应边相等).
点评 此题主要考查了全等三角形的应用,关键是掌握全等三角形对应边相等.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
14.下列各式从左边到右边的变形是因式分解的是( )
| A. | x2+2x+1=x(x+2)+1 | B. | 6x4y3=2x2y2•3x2y | ||
| C. | (x+1)(x-1)=x2-1 | D. | x2-4x+4=(x-2)2 |
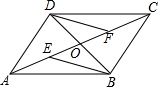 如图所示,四边形ABCD的对角线AC、BD交于点O,若OE=OF,DF∥BE.
如图所示,四边形ABCD的对角线AC、BD交于点O,若OE=OF,DF∥BE. 如图,△ABC是直角三角形,∠ACB=90°,∠B=30°,以点C为旋转中心,将△ABC旋转到△A′B′C′的位置,且使A′B′经过点A.
如图,△ABC是直角三角形,∠ACB=90°,∠B=30°,以点C为旋转中心,将△ABC旋转到△A′B′C′的位置,且使A′B′经过点A.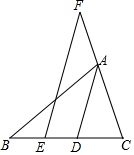 如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD.
如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD.