题目内容
18.(1)四边形ABCD为矩形,△BCE中,BE=CE,请用无刻度的直尺作出△BCE的高EH;(2)四边形ABCD为矩形,E,F为AD上的两点,且∠ABE=∠DCF,请用无刻度的直尺找到BC的中点P.
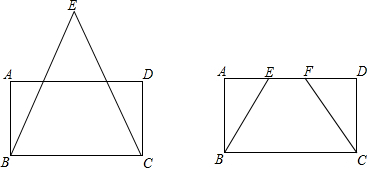
分析 (1)作矩形的对角线,它们相交于点O,连接EO并延长交BC于H,则EH⊥BC;
(2)分别延长BE和CF,它们相交于点M,再作矩形的对角线,它们相交于点O,连接MO并延长交BC于P,则BP=CP.
解答 解:(1)如图1,EH为所作;
(2)如图2,点P为所作.
点评 本题考查了作图-法则作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
6.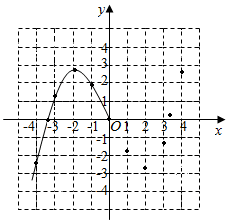 某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.
某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.
(1)请补全函数图象;
(2)方程$\frac{1}{6}$x3-2x=-2实数根的个数为3;
(3)观察图象,写出该函数的两条性质.
 某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.
某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.| x | … | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
| y | … | -$\frac{8}{3}$ | -$\frac{7}{48}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | $\frac{11}{6}$ | 0 | -$\frac{11}{6}$ | -$\frac{8}{3}$ | -$\frac{3}{2}$ | $\frac{7}{48}$ | $\frac{8}{3}$ | … |
(2)方程$\frac{1}{6}$x3-2x=-2实数根的个数为3;
(3)观察图象,写出该函数的两条性质.
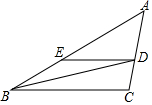 如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°.
如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°.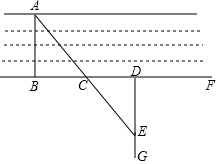 小明家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C、D使CD=CB,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段DE的长度就是AB的长.
小明家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C、D使CD=CB,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段DE的长度就是AB的长.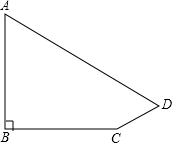 如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=16米,斜坡坡面上的影长CD=4米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.($\sqrt{3}$=1.732,精确到1米)
如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=16米,斜坡坡面上的影长CD=4米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.($\sqrt{3}$=1.732,精确到1米) 己知直线1:y=(m-3)x+m+2经过第一、二、四象限,则m的取值范围是( )
己知直线1:y=(m-3)x+m+2经过第一、二、四象限,则m的取值范围是( )



 根据图中各点的位置,在数轴上A,B,C,D四个点中,其中表示的数与4-$\sqrt{28}$的结果最接近的点是B.
根据图中各点的位置,在数轴上A,B,C,D四个点中,其中表示的数与4-$\sqrt{28}$的结果最接近的点是B.