题目内容

19．在平面直角坐标系中，点P（2x+4，x-3）在第四象限，则x的取值范围表示在数轴上，正确的是（　　）
A．B．
C．D．

分析 根据第四象限内点的坐标符号特点列出关于x的不等式组，分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．

解答 解：根据题意，得：$\left\{\begin{array}{l}{2x+4＞0}&{①}\\{x-3＜0}&{②}\end{array}\right.$，
解不等式①，得：x＞-2，
解不等式②，得：x＜3，
则不等式组的解集为-2＜x＜3，
故选：A．

点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．

练习册系列答案
相关题目
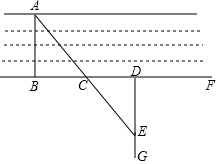9．小明家门前有一条小河，村里准备在河面上架上一座桥，但河宽AB无法直接测量，爱动脑的小明想到了如下方法：在与AB垂直的岸边BF上取两点C、D使CD=CB，再引出BF的垂线DG，在DG上取一点E，并使A、C、E在一条直线上，这时测出线段DE的长度就是AB的长．
（1）按小明的想法填写题目中的空格；
（2）请完成推理过程．
10．己知直线1：y=（m-3）x+m+2经过第一、二、四象限，则m的取值范围是（　　）
A．B．C．D．
7．根据图中各点的位置，在数轴上A，B，C，D四个点中，其中表示的数与4-$\sqrt{28}$的结果最接近的点是B．
14．解方程：
（1）2x2=50
（2）（x-1）3=-27．
4．某文具店销售功能相同的A、B两种品牌的计算器，若购买2个A品牌和3个B品牌的计算器共需96元；购买3个A品牌和2个B品牌的计算器共需94元．
（1）求这两种品牌计算器的单价；
（2）该商店在学校开学时对这两种计算器开展了促销活动，具体办法如下：A品牌计算器全部按原价的八折销售；购买B品牌计算器不超过5个，则按原价销售，若超过5个，在超出的部分按原价的七折销售，七年级部分同学准备集体购买同一品牌的计算器，且购买数量超过5个，则他们购买哪一种计算器更合算？说明理由．
11．某种品牌的洗面奶，外包装标明净含量为500±10g，表明了这种洗面奶的净含量x的范围是（　　）
A．490＜x＜510B．490≤x≤510C．490＜x≤510D．490≤x＜510
8．关于x的一元二次方程（n+1）x2+x+n2=1的一个根是0，求n的值．
9．点P（2a-1，a+2）在x轴上，则点P的坐标为（-5，0）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网