题目内容
1.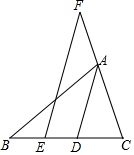 如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD.
如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD.(1)求∠BAF的度数.
(2)求∠F的度数.
分析 (1)根据外角的性质即可得到结论;
(2)根据角平分线的定义得到∠DAC=$\frac{1}{2}$BAC=35°,根据平行线的性质即可得到结论.
解答 解:(1)∵∠BAF=∠B+∠C,
∵∠B=40°,∠C=70°,
∴∠BAF=110°;
(2)∵∠BAF=110°,
∴∠BAC=70°,
∵AD是△ABC的角平分线,
∴∠DAC=$\frac{1}{2}$BAC=35°,
∵EF∥AD,
∴∠F=∠DAC=35°.
点评 本题考查了三角形外角的性质,平行线的性质,三角形的内角和,角平分线的定义,熟练掌握三角形外角的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.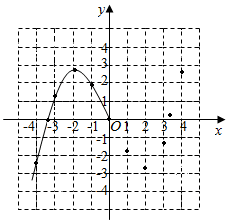 某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.
某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.
(1)请补全函数图象;
(2)方程$\frac{1}{6}$x3-2x=-2实数根的个数为3;
(3)观察图象,写出该函数的两条性质.
 某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.
某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.| x | … | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
| y | … | -$\frac{8}{3}$ | -$\frac{7}{48}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | $\frac{11}{6}$ | 0 | -$\frac{11}{6}$ | -$\frac{8}{3}$ | -$\frac{3}{2}$ | $\frac{7}{48}$ | $\frac{8}{3}$ | … |
(2)方程$\frac{1}{6}$x3-2x=-2实数根的个数为3;
(3)观察图象,写出该函数的两条性质.
11.某种品牌的洗面奶,外包装标明净含量为500±10g,表明了这种洗面奶的净含量x的范围是( )
| A. | 490<x<510 | B. | 490≤x≤510 | C. | 490<x≤510 | D. | 490≤x<510 |
 如图,一个大圆和四个面积相等的小圆,已知大圆半径等于小圆直径,小圆半径为a厘米,那么阴影部分的面积为πa2平方厘米.
如图,一个大圆和四个面积相等的小圆,已知大圆半径等于小圆直径,小圆半径为a厘米,那么阴影部分的面积为πa2平方厘米.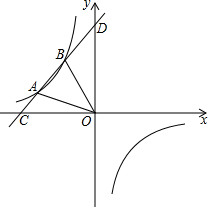 如图,直线y=mx+n(m≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于A、B两点,直线AB与坐标轴分别交于C、D两点,连接OA,若OA=2$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B(-3,b).
如图,直线y=mx+n(m≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于A、B两点,直线AB与坐标轴分别交于C、D两点,连接OA,若OA=2$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B(-3,b).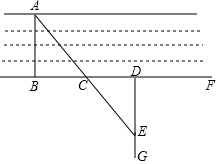 小明家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C、D使CD=CB,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段DE的长度就是AB的长.
小明家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C、D使CD=CB,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段DE的长度就是AB的长. 己知直线1:y=(m-3)x+m+2经过第一、二、四象限,则m的取值范围是( )
己知直线1:y=(m-3)x+m+2经过第一、二、四象限,则m的取值范围是( )


