题目内容
 如图,菱形OABC的顶点是坐标原点,顶点A在x轴的正半轴上,顶点B,C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′处和点C′处,且∠BDB′=120°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为
如图,菱形OABC的顶点是坐标原点,顶点A在x轴的正半轴上,顶点B,C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′处和点C′处,且∠BDB′=120°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为考点:菱形的性质,待定系数法求反比例函数解析式,翻折变换(折叠问题)
专题:
分析:连接AC,求出△BAC是等边三角形,推出AC=AB,求出△DC′B′是等边三角形,推出C′D=B′D,得出CB=BD=B′C′,推出A和D重合,连接BB′交x轴于E,求出AB′=AB=2,∠B′AE=60°,求出B′的坐标是(3,-
),设经过点B′反比例函数的解析式是y=
,代入求出即可.
| 3 |
| k |
| x |
解答:解:连接AC,
∵四边形OABC是菱形,
∴CB=AB,∠CBA=∠AOC=60°,
∴△BAC是等边三角形,
∴AC=AB,
∵将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,
∴BD=B′D,CD=C′D,∠DB′C′=∠ABC=60°,
∵∠BDB′=60°,
∴∠DC′B′=60°,
∴△DC′B′是等边三角形,
∴C′D=B′D,
∴CB=BD=B′C′,
即A和D重合,
连接BB′交x轴于E,
则AB′=AB=2,∠B′AE=
∠BDB′=60°,
在Rt△AB′E中,∠B′AE=60°,AB′=2,
∴AE=1,B′E=
,OE=2+1=3,
即B′的坐标是(3,-
),
设经过点B′反比例函数的解析式是y=
,
代入得:k=-3
,
即y=-
.
故答案为:y=-
.
∵四边形OABC是菱形,
∴CB=AB,∠CBA=∠AOC=60°,
∴△BAC是等边三角形,
∴AC=AB,
∵将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,

∴BD=B′D,CD=C′D,∠DB′C′=∠ABC=60°,
∵∠BDB′=60°,
∴∠DC′B′=60°,
∴△DC′B′是等边三角形,
∴C′D=B′D,
∴CB=BD=B′C′,
即A和D重合,
连接BB′交x轴于E,
则AB′=AB=2,∠B′AE=
| 1 |
| 2 |
在Rt△AB′E中,∠B′AE=60°,AB′=2,
∴AE=1,B′E=
| 3 |
即B′的坐标是(3,-
| 3 |
设经过点B′反比例函数的解析式是y=
| k |
| x |
代入得:k=-3
| 3 |
即y=-
3
| ||
| x |
故答案为:y=-
3
| ||
| x |
点评:此题考查了折叠性质,菱形性质,等边三角形的性质和判定的应用,主要考查学生的计算能力,题目比较好.

练习册系列答案
相关题目
在平面直角坐标系中,点A位于y轴的左侧,x轴的上方,并且距离每个坐标轴都是4个单位长度,则点A的坐标是( )
| A、(4,4) |
| B、(4,-4) |
| C、(-4,4) |
| D、(-4,-4) |
 如图,点A是直线y=2x上一动点,以A为顶点的抛物线y=(x-m)2+h交直线y=2x于另一点E,交y轴于点F,抛物线的对称轴交x轴于点B,交直线EF于点C(点A,E,F两两不重合).
如图,点A是直线y=2x上一动点,以A为顶点的抛物线y=(x-m)2+h交直线y=2x于另一点E,交y轴于点F,抛物线的对称轴交x轴于点B,交直线EF于点C(点A,E,F两两不重合). △ABC中,D在BC上,且AB=AC=BD,∠1=30°,∠ADB=
△ABC中,D在BC上,且AB=AC=BD,∠1=30°,∠ADB= 如图,AM∥NP,AM=2,MN=1,NP=1,∠AMN=150°,正方形ABCD的边长为1.它沿着AM-MN-NP作无滑动翻转,至它的一个顶点第一次与P重合为止,则在此过程中,正方形的中心O运动的路线长为
如图,AM∥NP,AM=2,MN=1,NP=1,∠AMN=150°,正方形ABCD的边长为1.它沿着AM-MN-NP作无滑动翻转,至它的一个顶点第一次与P重合为止,则在此过程中,正方形的中心O运动的路线长为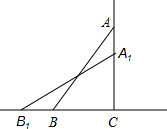 如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)
如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)