题目内容
已知反比例函数y=
，当x≥3时，则y的取值范围是 ．
| 6 |
| x |
考点：反比例函数的性质
专题：
分析：先根据反比例函数的性质判断出函数的增减性，再求出x=3时y的值即可得出结论．
解答：解：∵反比例函数y=
中，k=6＞0，
∴此函数图象的两个分支位于一、三象限，且在每一象限内y随x的增大而减小，
∵当x=3时，y=2，
∴当x≥3时，0＜y≤2．
故答案为：0＜y≤2；
| 6 |
| x |
∴此函数图象的两个分支位于一、三象限，且在每一象限内y随x的增大而减小，
∵当x=3时，y=2，
∴当x≥3时，0＜y≤2．
故答案为：0＜y≤2；
点评：本题考查的是反比例函数的性质，熟知反比例函数的增减性是解答此题的关键．
练习册系列答案
相关题目
如图，某人在山脚A处测得一座塔BD的塔尖点B的仰角为60°，沿山坡向上走到P处再测得点B的仰角为45°，已知坡面AP=40米，坡角∠PAC=30°，且D、A、C在同一条直线上，求塔BD的高度（测角仪的高度忽略不计，结果用根号表示）
如图，菱形OABC的顶点是坐标原点，顶点A在x轴的正半轴上，顶点B，C均在第一象限，OA=2，∠AOC=60°．点D在边AB上，将四边形ODBC沿直线OD翻折，使点B和点C分别落在这个坐标平面内的点B′处和点C′处，且∠BDB′=120°．若某反比例函数的图象经过点B′，则这个反比例函数的解析式为
如图，BD是⊙O的直径，点A、C在圆周上，∠CBD=20°，则∠A的度数为
如图，正方形ABCD中，分别以B、D为圆心，以正方形的边长a为半径画弧，形成树叶形（阴影部分）图案，则树叶形图案的面积为下列运算，正确的是（ ）
| A、2a+3b=5ab |
| B、a3•a2=a5 |
| C、a6÷a2=a3 |
| D、a3+a2=a5 |
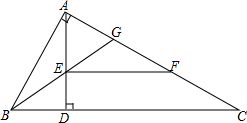如图，Rt△ABC中，∠BAC=90°，AD⊥BC于D，BG平分∠ABC，EF∥BC交AC于F．