题目内容
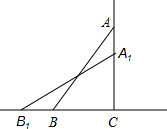 如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)
如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)考点:勾股定理的应用
专题:
分析:在直角三角形ABC中,已知AB,BC根据勾股定理即可求AC的长度,根据AC=AA1+CA1即可求得CA1的长度,在直角三角形A1B1C中,已知AB=A1B1,CA1即可求得CB1的长度,根据BB1=CB1-CB即可求得BB1的长度.
解答:解:在直角△ABC中,已知AB=13m,BC=5m,
则AC=
=12(m),
∵AC=AA1+CA1
∴CA1=11m,
∵在直角△A1B1C中,AB=A1B1,且A1B1为斜边,
∴CB1=
=4
(m),
∴BB1=CB1-CB=4
m-5m≈1.93m.
答:梯足向外移动了1.93m.
则AC=
| 132-52 |
∵AC=AA1+CA1
∴CA1=11m,
∵在直角△A1B1C中,AB=A1B1,且A1B1为斜边,
∴CB1=
| (A1B1)2-(CA1)2 |
| 3 |
∴BB1=CB1-CB=4
| 3 |
答:梯足向外移动了1.93m.
点评:本题考查了勾股定理在实际生活中的应用,考查了勾股定理在直角三角形中的正确运用,本题中求CB1的长度是解题的关键.

练习册系列答案
相关题目
下列运算,正确的是( )
| A、2a+3b=5ab |
| B、a3•a2=a5 |
| C、a6÷a2=a3 |
| D、a3+a2=a5 |
 如图,菱形OABC的顶点是坐标原点,顶点A在x轴的正半轴上,顶点B,C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′处和点C′处,且∠BDB′=120°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为
如图,菱形OABC的顶点是坐标原点,顶点A在x轴的正半轴上,顶点B,C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′处和点C′处,且∠BDB′=120°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为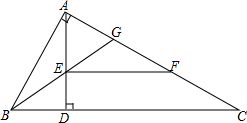 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC交AC于F.
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC交AC于F.
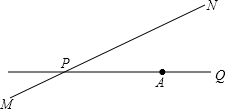 如图,公路MN和公路PQ在点P处交汇且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪音的影响(已知拖拉机的速度为18km/h),那么拖拉机在公路MN上眼PN方向行驶时,学校收到噪声影响的时间为多少秒?
如图,公路MN和公路PQ在点P处交汇且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪音的影响(已知拖拉机的速度为18km/h),那么拖拉机在公路MN上眼PN方向行驶时,学校收到噪声影响的时间为多少秒?