题目内容
 如图,在四边形ABCD中,∠BAD=120°,∠C=60°,AB=1,AD=DC=2,则BC边的长为
如图,在四边形ABCD中,∠BAD=120°,∠C=60°,AB=1,AD=DC=2,则BC边的长为考点:全等三角形的判定与性质
专题:
分析:连结BD,作DM⊥AB于M,DN⊥BC于N,根据三角函数可求AM=1,DM=
,DN=
,NC=1,通过HL证明Rt△BDM≌Rt△BDN,根据全等三角形的性质可得BN=BM,再根据线段的和差关系即可求解.
| 3 |
| 3 |
解答:
 解:连结BD,作DM⊥AB于M,DN⊥BC于N,
解:连结BD,作DM⊥AB于M,DN⊥BC于N,
∵∠BAD=120°,
∴∠MAD=180°-120°=60°,
∵AD=2,
∴AM=1,DM=
,
∵∠C=60°,
∴DN=
,NC=1,
在Rt△BDM与Rt△BDN中,
,
∴Rt△BDM≌Rt△BDN(HL),
∴BN=BM=1+1=2,
∴BC=BN+NC=3.
故答案为:3.
 解:连结BD,作DM⊥AB于M,DN⊥BC于N,
解:连结BD,作DM⊥AB于M,DN⊥BC于N,∵∠BAD=120°,
∴∠MAD=180°-120°=60°,
∵AD=2,
∴AM=1,DM=
| 3 |
∵∠C=60°,
∴DN=
| 3 |
在Rt△BDM与Rt△BDN中,
|
∴Rt△BDM≌Rt△BDN(HL),
∴BN=BM=1+1=2,
∴BC=BN+NC=3.
故答案为:3.
点评:本题考查了全等三角形的判定与性质,三角函数,关键是作出辅助线,通过HL证明Rt△BDM≌Rt△BDN.

练习册系列答案
相关题目
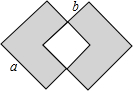 如图是两个大小相同的正方形,他们重合的部分(空白的部分)是一个小正方形,则阴影部分的面积为( )
如图是两个大小相同的正方形,他们重合的部分(空白的部分)是一个小正方形,则阴影部分的面积为( )| A、2a2-(a-b)2 |
| B、2a2-2(a-b)2 |
| C、(a-b)2 |
| D、2a2-b2 |
 如图,已知等边△ABC的边长为6,点D为AC的中点,点E为BC的中点,点P为BD上一点,则PE+PC的最小值为( )
如图,已知等边△ABC的边长为6,点D为AC的中点,点E为BC的中点,点P为BD上一点,则PE+PC的最小值为( )| A、3 | ||
B、3
| ||
C、2
| ||
D、3
|
-2015的相反数是( )
| A、2015 | ||
| B、-2015 | ||
C、
| ||
D、-
|
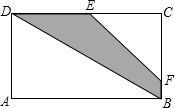 如图所示,长方形长为8cm,宽为4cm,E是线段CD的中点.
如图所示,长方形长为8cm,宽为4cm,E是线段CD的中点. 如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AE∥BC,AE∥BD.请完成下列证明过程.
如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AE∥BC,AE∥BD.请完成下列证明过程.