题目内容
 如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AE∥BC,AE∥BD.请完成下列证明过程.
如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AE∥BC,AE∥BD.请完成下列证明过程.证明:∵∠5=∠6
∴AB∥CE
∴∠3=∠BDC
∵∠3=∠4
∴∠4=∠BDC
∴
∴∠2=∠ADB
∵∠1=∠2,∴∠1=∠ADB,∴AD∥BC
考点:平行线的判定与性质
专题:推理填空题
分析:根据平行线的判定提出AB∥CE,求出∠3=∠BDC=∠4,根据平行线的判定得出AE∥BD,根据平行线的性质得出∠2=∠ADB,求出∠1=∠ADB,根据平行线的判定得出即可.
解答:
证明:∵∠5=∠6,
∴AB∥CE(内错角相等,两直线平行),
∴∠3=∠BDC(两直线平行,内错角相等),
∵∠3=∠4,
∴∠4=∠BDC(等量代换),
∴AE∥BD(同位角相等,两直线平行),
∴∠2=∠ADB,
∵∠1=∠2,
∴∠1=∠ADB,
∴AD∥BC(内错角相等,两直线平行),
故答案为:(内错角相等,两直线平行),(两直线平行,内错角相等),(等量代换),AE,(同位角相等,两直线平行),(内错角相等,两直线平行).
∴AB∥CE(内错角相等,两直线平行),
∴∠3=∠BDC(两直线平行,内错角相等),
∵∠3=∠4,
∴∠4=∠BDC(等量代换),
∴AE∥BD(同位角相等,两直线平行),
∴∠2=∠ADB,
∵∠1=∠2,
∴∠1=∠ADB,
∴AD∥BC(内错角相等,两直线平行),
故答案为:(内错角相等,两直线平行),(两直线平行,内错角相等),(等量代换),AE,(同位角相等,两直线平行),(内错角相等,两直线平行).
点评:本题考查了平行线的性质和判定的应用,能综合运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
 如图,在四边形ABCD中,∠BAD=120°,∠C=60°,AB=1,AD=DC=2,则BC边的长为
如图,在四边形ABCD中,∠BAD=120°,∠C=60°,AB=1,AD=DC=2,则BC边的长为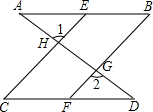 如图,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,如果∠1=∠2,∠B=∠C,试说明∠A=∠D,并写出每一步推理的依据.
如图,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,如果∠1=∠2,∠B=∠C,试说明∠A=∠D,并写出每一步推理的依据. 如图,点B、E、C、F在同一条直线上,∠A=∠D=90°,AB=DF,BE=CF,AC与DE相交于点M,求证:ME=MC.
如图,点B、E、C、F在同一条直线上,∠A=∠D=90°,AB=DF,BE=CF,AC与DE相交于点M,求证:ME=MC. 如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC.∠B与∠E相等吗?为什么?
如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC.∠B与∠E相等吗?为什么? 在△ABC中,∠C=90°,BC=3,∠A=30°,解这个直角三角形.
在△ABC中,∠C=90°,BC=3,∠A=30°,解这个直角三角形.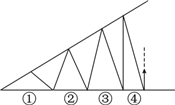 如图,不断地将楔形木片分成面积相等的三角形.这时,任意地确定左端最初的三角形后,后面的尺寸自然地就确定了.设下侧的边为①、②、③,等等,问:
如图,不断地将楔形木片分成面积相等的三角形.这时,任意地确定左端最初的三角形后,后面的尺寸自然地就确定了.设下侧的边为①、②、③,等等,问: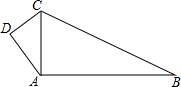 如图,∠ADC=90°,AB=24,BC=26,DC=6,AD=8,
如图,∠ADC=90°,AB=24,BC=26,DC=6,AD=8,