题目内容
如图，已知等边△ABC的边长为6，点D为AC的中点，点E为BC的中点，点P为BD上一点，则PE+PC的最小值为（ ）| A、3 | ||
B、3
| ||
C、2
| ||
D、3
|
考点：轴对称-最短路线问题
专题：
分析：由题意可知点A、点C关于BD对称，连接AE交BD于点P，由对称的性质可得，PA=PC，故PE+PC=AE，由两点之间线段最短可知，AE即为PE+PC的最小值．
解答：
解：∵△ABC是等边三角形，点D为AC的中点，点E为BC的中点，
∴BD⊥AC，EC=3，
连接AE，线段AE的长即为PE+PC最小值，
∵点E是边BC的中点，
∴AE⊥BC，
∴AE=
=
=3
，
∴PE+PC的最小值是3
．
故选D．
解：∵△ABC是等边三角形，点D为AC的中点，点E为BC的中点，∴BD⊥AC，EC=3，
连接AE，线段AE的长即为PE+PC最小值，
∵点E是边BC的中点，
∴AE⊥BC，
∴AE=
| AC2-EC2 |
| 62-32 |
| 3 |
∴PE+PC的最小值是3
| 3 |
故选D．
点评：本题考查的是轴对称-最短路线问题，熟知等边三角形的性质是解答此题的关键．
练习册系列答案
相关题目
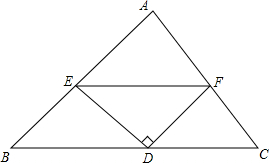如图，已知△ABC中，D是BC的中点，ED⊥DF．求证：BE+CF＞EF．
如图，在四边形ABCD中，∠BAD=120°，∠C=60°，AB=1，AD=DC=2，则BC边的长为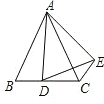
在△ABC中，AB=AC，点D是直线BC上一点（不与点B、C重合）以AD为一边，在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
如图，点A、C、D、F在同一条直线上，AB=FE，BC=ED，AD=FC．∠B与∠E相等吗？为什么？