题目内容
11. 如图,E是正方形ABCD的BC边上一点,过AE上点P作FG⊥AC,分别交AB、CD于F、G,求证:FG=AE.
如图,E是正方形ABCD的BC边上一点,过AE上点P作FG⊥AC,分别交AB、CD于F、G,求证:FG=AE.
分析 过点F作FH⊥DC,交AE于点M,由正方形的性质以及已知条件易证△ABE≌△FHG,进而可证明FG=AE.
解答 解:
过点F作FH⊥DC,交AE于点M,
∵四边形ABCD是正方形,
∴AB=BC=FH,∠ABE=∠FHG=90°,
∴∠BAE+∠FMA=90°,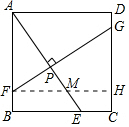
∵FG⊥AC,
∴∠GFH+∠FMA=90,
∴∠BAE=∠FMA,
在△ABE和△FHG中,
$\left\{\begin{array}{l}{∠BAE=∠FMA}\\{AB=FH}\\{∠ABC=∠FHG=90°}\end{array}\right.$,
∴△ABE≌△FHG,
∴AE=FG.
点评 本题考查了全等三角形的判定与性质,利用了正方形的性质,全等三角形的判定与性质,余角的性质,直角三角形的判定,垂线的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若m<0,n>0,则一次函数y=mx-n的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.在直角三角形中,自锐角顶点所引的两条中线长为$\sqrt{10}$和$\sqrt{35}$,那么这个直角三角形的斜边长为( )
| A. | 6 | B. | 7 | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{7}$ |
3.为增强居民节约用水意识,深圳市在2011年开始对供水范围内的居民用水实行“阶梯收费”,具体收费标准如下表:
某户居民四月份用水10米3时,缴纳水费23元.
(1)求a的值;
(2)若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.
| 一户居民一个月用水量即为x米3 | 水费单价 (单位:元/米3) |
| x≤22 | a |
| 超出22米3的部分 | a+1.1 |
(1)求a的值;
(2)若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.
 如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.
如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.