题目内容
13.已知菱形的周长是36cm,一条对角线的长是9cm,那么这个菱形的两个相邻内角的度数分别是60°,120°.分析 如图,菱形ABCD的周长为36cm,对角线BD=9cm,根据菱形的性质得AB=BC=CD=AD=9cm,则AB=BD=AD=BC=CD,于是可判断△ABD、△BCD都为等边三角形,所以∠BAD=∠BCD=60°,则∠ABC=∠ADC=120°,即这个菱形的两个相邻内角的度数分别60°,120°.
解答 解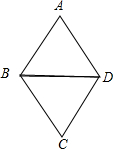 :如图,菱形ABCD的周长为36cm,对角线BD=9cm,
:如图,菱形ABCD的周长为36cm,对角线BD=9cm,
∵四边形ABCD为菱形,
∴AB=BC=CD=AD=9cm,
∵BD=9cm,
∴AB=BD=AD=BC=CD,
∴△ABD、△BCD都为等边三角形,
∴∠BAD=∠BCD=60°,
∴∠ABC=∠ADC=120°,
即这个菱形的两个相邻内角的度数分别60°,120°.
故答案为60°,120°.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.

练习册系列答案
相关题目
5.已知y=-x2-2x-2,其中x为实数,则y的取值范围是( )
| A. | -1≤y<0 | B. | y<0 | C. | y≤-1 | D. | 全体实数 |