题目内容
19.已知抛物线y=$\frac{1}{2}$x2+x+c与x轴没有交点.(1)求c的取值范围;
(2)试确定双曲线y=$\frac{c}{x}$经过的象限,并说明理由.
分析 (1)令y=$\frac{1}{2}$x2+x+c=0,根据抛物线y=$\frac{1}{2}$x2+x+c与x轴没有交点,则△<0,求出c的取值范围即可;
(2)根据反比例函数的性质直接得到双曲线y=$\frac{c}{x}$经过的象限.
解答 解:(1)令y=$\frac{1}{2}$x2+x+c=0,
∵抛物线y=$\frac{1}{2}$x2+x+c与x轴没有交点,
∴△=1-2c<0,
∴c>$\frac{1}{2}$;
(2)∵c>$\frac{1}{2}$,
∴双曲线y=$\frac{c}{x}$经过第一、三象限.
点评 本题主要考查了抛物线与x轴交点和反比例函数的性质的知识,解答本题要掌握抛物线与x轴没有交点,则△=b2-4ac<0,此题难度不大.

练习册系列答案
相关题目
14.某天同时同地,甲同学测得1m的测竿在地面上影长为0.8m,乙同学测得国旗旗杆在地面上的影长为9.6m,则国旗旗杆的长为( )
| A. | 10m | B. | 12m | C. | 13m | D. | 15m |
9.在-3,0,-π,8这四个数中,最小的数是( )
| A. | -3 | B. | 0 | C. | -π | D. | 8 |
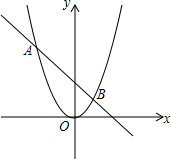 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx+c=0的解为无解.
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx+c=0的解为无解.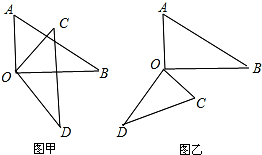 【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图甲所示的位置,请回答下面的问题.
【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图甲所示的位置,请回答下面的问题.