Question

16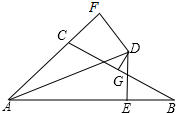．已知：∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB=6，AC=3．
（1）求证：△DBE≌△DCF；
（2）求BE的长．

Answer 1

分析 （1）连接CD、BD，由线段垂直平分线的性质可得CB=CD，由角平分线的性质可知DE=DF，利用HL可证明Rt△DBE≌Rt△DCF；
（2）由条件可证明Rt△ADF≌Rt△ADE，可得AF=AE，利用线段和差可得AE-BE=AC，又AE+BE=AB，可求得BE的长．

解答 解：
（1）证明：
连接CD、BD，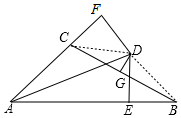

∵DG垂直平分BC，
∴BD=CD，
∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE=DF，
在Rt△DBE和Rt△DCF中
$\left\{\begin{array}{l}{DE=DF}\\{BD=CD}\end{array}\right.$
∴Rt△DBE≌Rt△DCF（HL）；
（2）∵AD平分∠BAC，
∴∠FAD=∠EAD，且由（1）可知DE=DF，
在Rt△ADF和Rt△ADE中，
$\left\{\begin{array}{l}{DF=DE}\\{AD=AD}\end{array}\right.$
∴Rt△ADF≌Rt△ADE（HL），
∴AE=AF，
又由（1）可知BE=CF，
∵AC=AF-CF，AB=AE+BE，
∴$\left\{\begin{array}{l}{AE-BE=3}\\{AE+BE=6}\end{array}\right.$，解得BE=1.5．

点评 本题主要考查全等三角形的判定和性质，构造三角形全等是解题的关键，注意角平分线和线段垂直平分线性质的应用．