题目内容
7.(1)计算:(-$\frac{1}{3}}$)-1-2÷$\sqrt{16}$+(3.14-π)0×sin30°.(2)先化简,再求值:$\frac{{a}^{2}-6ab+9{b}^{2}}{{a}^{2}-2ab}$÷($\frac{5{b}^{2}}{a-2b}$-a-2b)-$\frac{1}{a}$,其中a,b满足$\left\{\begin{array}{l}a+b=4\\ a-b=2.\end{array}$
(3)解方程:$\frac{3}{{x}^{2}+2x}$-$\frac{1}{{x}^{2}-2x}$=0.
分析 (1)原式利用零指数幂、负整数指数幂法则,以及特殊角的三角函数值计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则变形,同时利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,求出方程组的解得到a与b的值,代入计算即可求出值;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=-3-$\frac{1}{2}$+$\frac{1}{2}$=-3;
(2)原式=$\frac{(a-3b)^{2}}{a(a-2b)}$÷$\frac{5{b}^{2}-(a+2b)(a-2b)}{a-2b}$-$\frac{1}{a}$=$\frac{(a-3b)^{2}}{a(a-2b)}$•$\frac{a-2b}{-(a+3b)(a-3b)}$-$\frac{1}{a}$=-$\frac{a-3b}{a(a+3b)}$-$\frac{1}{a}$=$\frac{-a+3b-a-3b}{a(a+3b)}$=-$\frac{2}{a+3b}$,
方程组$\left\{\begin{array}{l}{a+b=4①}\\{a-b=2②}\end{array}\right.$,
①+②得:2a=6,即a=3,
①-②得:2b=2,即b=1,
则原式=-$\frac{1}{3}$;
(3)去分母得:3x-6-x-2=0,
解得:x=4,
经检验x=4是分式方程的解.
点评 此题考查了解分式方程,实数的运算,以及分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.有10筐白菜,以每筐15kg为准,超过的千克数记作正数,不足的千克数记作负数,称重后的记录如表:
求这10筐白菜一共多少千克?
| 筐数 | 2 | 4 | 3 | 1 |
| 与标准重量比较 | +0.5 | -0.4 | +0.2 | -0.3 |
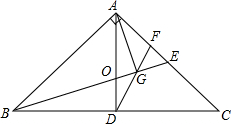 Rt△ABC中,∠BAC=90°,AB=AC,D是BC中点,∠FGE=45°.
Rt△ABC中,∠BAC=90°,AB=AC,D是BC中点,∠FGE=45°.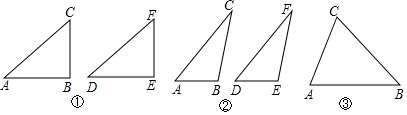
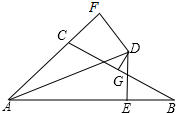 已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3.
已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3.