题目内容
8.将分式(1+$\frac{3}{a-1}$)÷$\frac{a+2}{{a}^{2}-1}$进行化简,并在-2,-1,0,1选择一个合适的数,求出原式的值.分析 先将分式化简,然后求出分式有意义的条件即可判断选择哪一个数代入原式.
解答 解:原式=$({1+\frac{3}{a-1}})÷\frac{a+2}{{{a^2}-1}}$=a+1
∵$\left\{\begin{array}{l}{a-1≠0}\\{{a}^{2}-1≠0}\\{a+2≠0}\end{array}\right.$,
∴a≠±1且a≠-2
当a=0时,原式=a+1=1
点评 本题考查分式化简,涉及因式分解,分式的性质,分式有意义的条件.

练习册系列答案
相关题目
17.有10筐白菜,以每筐15kg为准,超过的千克数记作正数,不足的千克数记作负数,称重后的记录如表:
求这10筐白菜一共多少千克?
| 筐数 | 2 | 4 | 3 | 1 |
| 与标准重量比较 | +0.5 | -0.4 | +0.2 | -0.3 |
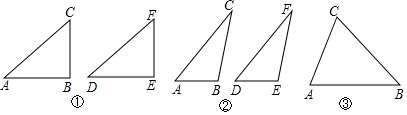
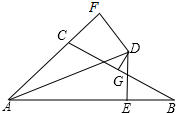 已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3.
已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3.
