题目内容
6. 如图,已知AB是⊙O的直径,C,D是⊙O上两点,∠CDB=45°.过点C作CE∥AB交DB的延长线于点E.
如图,已知AB是⊙O的直径,C,D是⊙O上两点,∠CDB=45°.过点C作CE∥AB交DB的延长线于点E.(1)求证:CE是⊙O的切线;
(2)若cos∠CED=$\frac{1}{3}$,BD=6,求⊙O的直径.
分析 (1)要证CE是⊙O的切线,只要证明∠OCE=90°,根据,∠CDB=45°,CE∥AB可以求得∠OCE=90°,从而可以解答本题;
(2)要求⊙O的直径,根据CE∥AB,cos∠CED=$\frac{1}{3}$,BD=6,可以求得AB的长,本题得以解决.
解答 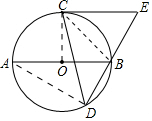 (1)证明:连接BC、CO,如右图所示,
(1)证明:连接BC、CO,如右图所示,
∵AB是⊙O的直径,C,D是⊙O上两点,∠CDB=45°,
∴∠COB=2∠CDB=90°,
∵CE∥AB,
∴∠COB+∠OCE=180°,
∴∠OCE=90°,
即CE是⊙O的切线;
(2)连接AD,如右上图所示,
∵CE∥AB,
∴∠CED=∠ABD,
∵cos∠CED=$\frac{1}{3}$,BD=6,AB是⊙O的直径,
∴∠ADB=90°,cos∠ABD=$\frac{1}{3}$,
∴$\frac{BD}{AB}=\frac{1}{3}$,
∴AB=18,
即⊙O的直径是18.
点评 本题考查切线的判定、圆周角定理、解直角三角形,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.有10筐白菜,以每筐15kg为准,超过的千克数记作正数,不足的千克数记作负数,称重后的记录如表:
求这10筐白菜一共多少千克?
| 筐数 | 2 | 4 | 3 | 1 |
| 与标准重量比较 | +0.5 | -0.4 | +0.2 | -0.3 |
19.已知A,B两市场各有蔬菜14吨,现向甲、乙两地运送蔬菜,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A市场到甲地的运费为50元/吨,到乙地的运费为30元/吨;从B市场到甲地的运费为60元/吨,到乙地的运费为45元/吨.
(1)设从A市场运往甲地x吨蔬菜,请完成表格:
(2)设总运费为W元,求W与x的函数关系式.
(3)怎样调运蔬菜才能使运费最少?
(1)设从A市场运往甲地x吨蔬菜,请完成表格:
| 运往甲地(单位:吨) | 运往乙地(单位:吨) | |
| A | x | 14-x |
| B | 15-x | x-1 |
(3)怎样调运蔬菜才能使运费最少?
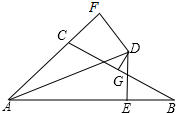 已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3.
已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3. 测量树AB的高度,它的影子一部分落在地面上,影长为1.5m,另一部分落在坡面上,影长为4m,此时竖立1m的标杆在地面上的影长为1.5m,在坡面上的影长为2m,则树高AB为3m.
测量树AB的高度,它的影子一部分落在地面上,影长为1.5m,另一部分落在坡面上,影长为4m,此时竖立1m的标杆在地面上的影长为1.5m,在坡面上的影长为2m,则树高AB为3m.