题目内容
7.⊙O的半径为1,弦AB=$\sqrt{2}$,弦AC=$\sqrt{3}$,则∠BAC度数为75°或15°.分析 连接OA,过O作OE⊥AB于E,OF⊥AC于F,根据垂径定理求出AE、FA值,根据解直角三角形的知识求出∠OAB和∠OAC,然后分两种情况求出∠BAC即可.
解答 解: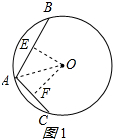 有两种情况:
有两种情况:
①如图1所示:连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=BE=$\frac{\sqrt{3}}{2}$,AF=CF=$\frac{\sqrt{2}}{2}$,
cos∠OAE=$\frac{AE}{OA}$=$\frac{\sqrt{3}}{2}$,cos∠OAF=$\frac{AF}{OA}$=$\frac{\sqrt{2}}{2}$,
∴∠OAE=30°,∠OAF=45°,∴∠BAC=30°+45°=75°;
②如图2所示:
连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=BE=$\frac{\sqrt{3}}{2}$,AF=CF=$\frac{\sqrt{2}}{2}$,
cos∠OAE═$\frac{AE}{OA}$=$\frac{\sqrt{3}}{2}$,cos∠OAF=$\frac{AF}{OA}$=$\frac{\sqrt{2}}{2}$,
∴∠OAE=30°,∠OAF=45°,
∴∠BAC=45°-30°=15°;
故答案为:75°或15°.
点评 本题考查了特殊角的三角函数值和垂径定理的应用.此题难度适中,解题的关键是根据题意作出图形,求出符合条件的所有情况.此题比较好,但是一道比较容易出错的题目.

练习册系列答案
相关题目
18.下列运算中,正确的是( )
| A. | a8÷a2=a4 | B. | (-m)2•(-m3)=-m5 | C. | x3+x3=x6 | D. | (a3)3=a6 |
15.下列各式中,最简二次根式是( )
| A. | $\sqrt{0.3}$ | B. | $\sqrt{12}$ | C. | $\sqrt{6{x}^{3}}$ | D. | $\sqrt{{x}^{2}+1}$ |
 实数,在数轴上的位置如图所示,则化简|a-b|+a的结果为b.
实数,在数轴上的位置如图所示,则化简|a-b|+a的结果为b.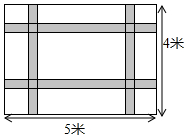 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.
如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.