题目内容
8.写出二元一次方程x+3y=9的一个正整数解:$\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.分析 本题是求不定方程的整数解,先将方程做适当变形,确定其中一个未知数的值,然后再求出另一个未知数的值.
解答 解:方程x+3y=9变形得x=9-3y.
要使x,y都是正整数,
则$\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$,
故答案可以是:$\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.
点评 本题考查了二元一次方程的解.二元一次方程有无数个解,但它的特殊解应用列举法先确定其中一个未知数的取值,再求出另一个未知数的值.

练习册系列答案
相关题目
19.下列关于x的方程中,没有实数根的是( )
| A. | 3x2+4x-2=0 | B. | 2x2+5=6x | C. | 3x2-2$\sqrt{6}$x+2=0 | D. | 2x2+mx-1=0 |
 如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=14cm,BC=12cm,S△ABC=52cm2,则DE=4cm.
如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=14cm,BC=12cm,S△ABC=52cm2,则DE=4cm. 已知:如图,在△ABC中,点D、E是边BC上的两点,AE=AD,∠1=∠2,BD=CE,求证:∠BAD=∠CAE.
已知:如图,在△ABC中,点D、E是边BC上的两点,AE=AD,∠1=∠2,BD=CE,求证:∠BAD=∠CAE.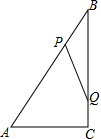 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.