题目内容
18.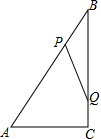 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.(1)用含t的代数式表示BP、BQ;
(2)是否存在某一时刻t的值,使△BPQ的面积是△BAC面积的$\frac{1}{4}$;
(3)若以B、P、Q为顶点的三角形与△ABC相似,求t的值.
分析 (1)直接用t表示出BP、BQ即可;
(2)作PD⊥BC于D,证得△BDF∽△BCA,进一步用t表示PD,利用三角形的面积建立方程求得答案即可;
(3)分两种情况讨论:当△BPQ∽△BAC时,当△BPQ∽△BCA时,再根据性质以及BP=5t,QC=4t,AB=10cm,BC=8cm,代入计算即可.
解答 解:(1)BP=5t,BQ=8-4t,
(2)如图,
∵AC=6cm,BC=8cm,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10cm,
作PD⊥BC于D,
∴∠BPD=∠C=90°,
∵∠B=∠B,
∴△BPD∽△BCA,
∴$\frac{BP}{BA}$=$\frac{PD}{AC}$,
∴$\frac{5t}{10}$=$\frac{PD}{6}$,
∴PD=3t,
∴$\frac{1}{2}$×(8-4t)×3t=$\frac{1}{2}$×8×6×$\frac{1}{4}$
解得:t1=t2=1,
当t=1时,使△BPQ的面积是△BAC面积的$\frac{1}{4}$;
(3)①当△BPQ∽△BAC时,
∵$\frac{BP}{BA}$=$\frac{BQ}{BC}$,BP=5t,QC=4t,AB=10cm,BC=8cm,
∴$\frac{5t}{10}$=$\frac{8-4t}{8}$,
∴t=1;
②当△BPQ∽△BCA时,
∵$\frac{BP}{BC}$=$\frac{BQ}{BA}$,
∴$\frac{5t}{8}$=$\frac{8-4t}{10}$,
∴t=$\frac{32}{41}$,
∴t=1或$\frac{32}{41}$时,△BPQ与△ABC相似.
点评 本题考查了,一元二次方程的实际运用,相似三角形的性质:相似三角形的对应角相等,对应边的比相等.也考查了分类讨论的思想和利用代数法解决动点问题.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案| A. | 0 | B. | -$\frac{1}{2}$ | C. | -1 | D. | $\sqrt{3}$ |