题目内容
20.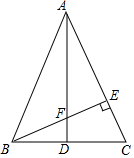 如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?
如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?
分析 根据等腰三角形的性质得到BC=2BD,AD⊥BC,由已知条件得到AF=BC,由垂直的定义得到∠AEF=∠BEC=90°,推出∠EAF=∠CBE,根据全等三角形的判定定理即可得到结论.
解答 解:△BCE与△AFE全等,
理由:∵AB=AC,AD是∠BAC的平分线,
∴BC=2BD,AD⊥BC,
∵AF=2BD,
∴AF=BC,
∵BE⊥AC于E,
∴∠AEF=∠BEC=90°,
∵∠AFE=∠BFD,
∴∠EAF=∠CBE,
在△BCE与△AFE中,$\left\{\begin{array}{l}{∠CBE=∠FAE}\\{∠AEF=∠BEC}\\{AF=BC}\end{array}\right.$,
∴△BCE≌△AFE.
点评 本题考查了全等三角形的判定,等腰三角形的性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
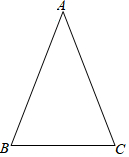 如图,在△ABC中,AB=AC,作AB的垂直平分线DE分别交AB,AC于点D,E,连接BE,则:
如图,在△ABC中,AB=AC,作AB的垂直平分线DE分别交AB,AC于点D,E,连接BE,则: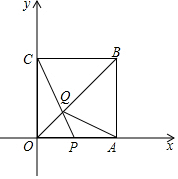 如图,将边长为4的正方形OABC置于平面直角坐标系中,点P在边OA上从O向A运动,连接CP交对角线OB于点Q,连接AQ.
如图,将边长为4的正方形OABC置于平面直角坐标系中,点P在边OA上从O向A运动,连接CP交对角线OB于点Q,连接AQ.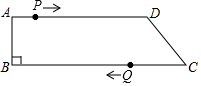 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.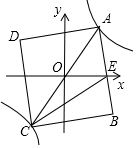 如图1,在平面直角坐标系中,正方形ABCD的两个顶点A,C在反比例函数y=$\frac{6}{x}$图象上,且对角线AC经过原点,AB与x轴交于点E,若△BCE的面积等于△AOE面积的2倍,则点A的坐标为($\sqrt{6}$,$\sqrt{6}$).
如图1,在平面直角坐标系中,正方形ABCD的两个顶点A,C在反比例函数y=$\frac{6}{x}$图象上,且对角线AC经过原点,AB与x轴交于点E,若△BCE的面积等于△AOE面积的2倍,则点A的坐标为($\sqrt{6}$,$\sqrt{6}$).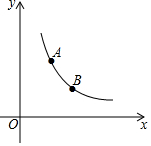 如图,已知点A(1,a)与点B(b,1)在反比例函数y=$\frac{2}{x}$(x>0)图象上,点P(m,0)是x轴上的任意一点,若△PAB的面积为2,此时m的值是-1或7.
如图,已知点A(1,a)与点B(b,1)在反比例函数y=$\frac{2}{x}$(x>0)图象上,点P(m,0)是x轴上的任意一点,若△PAB的面积为2,此时m的值是-1或7. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论: