题目内容
7.在平行四边形ABCD中,点E在CD上,点F在AB上,连接AE、CF、DF、BE,∠DAE=∠BCF.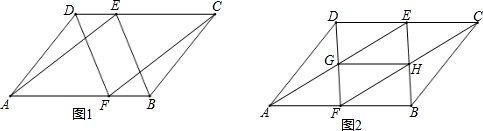
(1)如图1,求证:四边形DFBE是平行四边形;
(2)如图2,若E是CD的中点,连接GH,在不添加任何辅助线的情况下,请直接写出图2中以GH为边或以GH为对角线的所有平行四边形.
分析 (1)由平行四边形的性质得出AB∥CD,∠ADE=∠CBF,AD=BC,由ASA证明△ADE≌△CBF,得出DE=BF,即可得出四边形DFBE是平行四边形;
(2)由中点的定义得出DE=CE,由平行四边形的判定方法即可得出平行四边形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∠ADE=∠CBF,AD=BC,
在△ADE和△CBF中,$\left\{\begin{array}{l}{∠ADE=∠CBF}&{\;}\\{AD=BC}&{\;}\\{∠DAE=∠∠BCF}&{\;}\end{array}\right.$,
∴△ADE≌△CBF(ASA),
∴DE=BF,
又∵DE∥BF,
∴四边形DFBE是平行四边形;
(2)解:∵E是CD的中点,
∴DE=CE,
∴以GH为边的平行四边形有平行四边形GHFA、平行四边形GHBF、平行四边形GHED、平行四边形GHCE;
以GH为对角线的平行四边形有GFHE.
点评 本题考查了平行四边形的性质与判定、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等得出DE=BF是解决问题(1)的关键.

练习册系列答案
相关题目
8.对于直线、射线、线段,在下列各图中能相交的是( )
| A. |  | B. |  | C. |  | D. |  |
19.不解方程,判别方程2x2-2$\sqrt{2}$x+1=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |

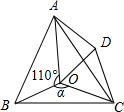 如图,点O是等边三角形ABC内一点,将△BOC绕点C顺时针方向旋转60°得到△ADC,连接OD,已知∠AOB=110°.
如图,点O是等边三角形ABC内一点,将△BOC绕点C顺时针方向旋转60°得到△ADC,连接OD,已知∠AOB=110°. 如图是一个数值转换机,如果输出结果为+1,那么输入的数x是-1.
如图是一个数值转换机,如果输出结果为+1,那么输入的数x是-1.