题目内容
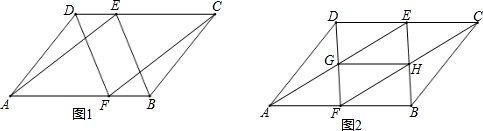
15.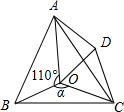 如图,点O是等边三角形ABC内一点,将△BOC绕点C顺时针方向旋转60°得到△ADC,连接OD,已知∠AOB=110°.
如图,点O是等边三角形ABC内一点,将△BOC绕点C顺时针方向旋转60°得到△ADC,连接OD,已知∠AOB=110°.(1)求证:△DOC是等边三角形;
(2)当α=180°时,试判断△DOA的形状,并说明理由;
(3)当α为多少度时,△DOA是等腰三角形.
分析 (1)由旋转的性质可知CO=CD,∠OCD=60°,可判断:△COD是等边三角形;
(2)由(1)可知∠COD=60°,当α=150°时,∠ADO=∠ADC-∠CDO,可判断△AOD为直角三角形;
(3)根据等腰三角形的性质,分别假设AO=AD,OA=OD,OD=AD,从而求出α.
解答 (1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠OCD=60°,CO=CD,
∴△OCD是等边三角形;
(2)解:△AOD为直角三角形.
理由:∵△COD是等边三角形.
∴∠ODC=60°,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠ADC=∠BOC=α,
∴∠ADC=∠BOC=150°,
∴∠ADO=∠ADC-∠CDO=150°-60°=90°,于是△AOD是直角三角形.
(3)解:①要使AO=AD,需∠AOD=∠ADO.
∵∠AOD=360°-∠AOB-∠COD-α=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠AOD=190°-α,∠ADO=α-60°,
∴∠OAD=180°-(∠AOD+∠ADO)=50°,
∴α-60°=50°
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.
∵190°-α=50°
∴α=140°.
综上所述:当α的度数为125°,或110°,或140°时,△AOD是等腰三角形.
点评 此题主要考查了等边三角形的性质与判定,以及等腰三角形的性质和旋转的性质等知识,根据旋转前后图形不变是解决问题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
3.下列函数中,y是x的反比例函数的是( )
| A. | y=3x | B. | y-3=2x | C. | xy=1 | D. | y=x2 |
5. 如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
 如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 70° |
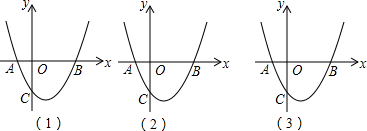
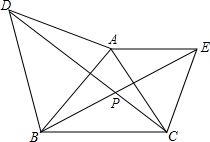 如图,△ABC中,分别以AB、AC为边向外作正△ABD、△ACE.试说明:
如图,△ABC中,分别以AB、AC为边向外作正△ABD、△ACE.试说明: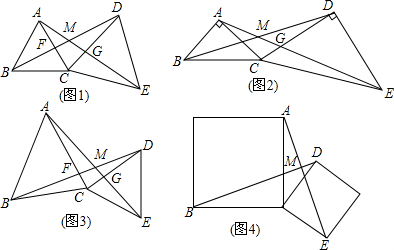
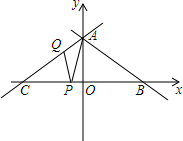 如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.
如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.