��Ŀ����
7����ͼ�٣���ƽ��ֱ������ϵ�У�������OABC�Ķ���A��B������ֱ�Ϊ��2��2������4��0������D��E�ֱ��DZ�OA��AB���е㣬��F���߶�DE���е㣬����D��������y=x2+2mx+n��m��nΪ�������Ķ���ΪP����1����D������Ϊ��1��1�����ú�m�Ĵ���ʽ��ʾnΪn=-2m��
��2����������y=x2+2mx+n����Bʱ����ͼ�ڣ�
���������������Ӧ�ĺ�������ʽ��
������M�ڸ��������ϣ���λ��x���·�����N��������OABC�ı��ϣ�����DE��MNΪ�Աߵ��ı�����ƽ���ı���ʱ�����N�����ꣻ
��3������P��������OABC�ı��ϻ��ڲ�����������y=x2+2mx+n���߶�EFû�й�����ʱ��ֱ��д��m��ȡֵ��Χ��
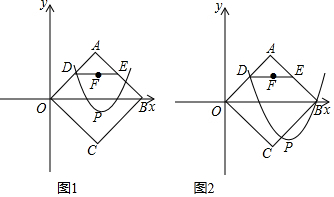
���� ��1�������е����깫ʽ���������D���꣬�ѵ�D������������ߵĽ���ʽ���ɽ�����⣮
��2���ٰѵ�B������������ߵĽ���ʽ���ɣ�
�ڹ۲�ͼ���֪��N��BC���ϣ�ֱ��BC�Ľ���ʽΪy=x-4����M��m��m2-$\frac{16}{3}$m+$\frac{16}{3}$������N��m+2��m2-$\frac{16}{3}$m+$\frac{16}{3}$�����ѵ�N�������ֱ��BC�Ľ���ʽ���ɣ�
��3���ֶԳ����ڵ�F����E�ұߣ��ֱ��г�����ʽ�飬�ⲻ��ʽ�鼴�ɽ�����⣮
��� �⣺��1����A��2��2����DO=DA��
��D��1��1����
��D��1��1������y=x2+2mx+n��1=1+2m+n��
��n=-2m��
�ʴ�Ϊ��1��1����n=-2m��
��2���١�y=x2+2mx-2m������B��4��0����
��0=16+8m-2m��
��m=-$\frac{8}{3}$��
�������ߵĽ���ʽΪy=x2-$\frac{16}{3}$x+$\frac{16}{3}$��
�ڹ۲�ͼ���֪��N��BC���ϣ�ֱ��BC�Ľ���ʽΪy=x-4��
��M��m��m2-$\frac{16}{3}$m+$\frac{16}{3}$������N��m+2��m2-$\frac{16}{3}$m+$\frac{16}{3}$����
�ѵ�N�������ֱ��BC�Ľ���ʽ�õ���m2-$\frac{16}{3}$m+$\frac{16}{3}$=m+2-4��
�����õ�3m2-19m+22=0��
���m=$\frac{19-\sqrt{97}}{6}$��$\frac{19+\sqrt{97}}{6}$��������
��N��$\frac{31-\sqrt{97}}{6}$��$\frac{7-\sqrt{97}}{6}$����
��3��������$\left\{\begin{array}{l}{-\frac{2m}{2}��\frac{3}{2}}\\{-m��2m+{m}^{2}}\\{-m��0}\end{array}\right.$��$\left\{\begin{array}{l}{-\frac{2m}{2}��2}\\{4+m��2m+{m}^{2}}\\{4+m��0}\end{array}\right.$��
���-$\frac{3}{2}$��m��0��$\frac{-1-\sqrt{17}}{2}$��m��-2��
���� ���⿼����κ����ۺ��⡢һ�κ���������ϵ����������ʽ���֪ʶ������Ĺؼ������Ӧ�ô���ϵ����ȷ����������ʽ��ѧ����ת����˼��˼�����⣬������ת��Ϊ����ʽ�������⣬�����п�ѹ���⣮

 ��ͼ��������A��B����ֱ��Ӧ����Ϊa��b�������н��۴�����ǣ�������
��ͼ��������A��B����ֱ��Ӧ����Ϊa��b�������н��۴�����ǣ�������| A�� | a+b��0 | B�� | ab��0 | C�� | |b|=b | D�� | |a|��|b| |
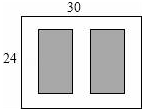 ��ͼ��ijС����һ�鳤Ϊ30m����Ϊ24m�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ480m2�������̵�֮�估�ܱ��п�����ȵ�����ͨ����������ͨ���Ŀ���Ϊ�����ף�
��ͼ��ijС����һ�鳤Ϊ30m����Ϊ24m�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ480m2�������̵�֮�估�ܱ��п�����ȵ�����ͨ����������ͨ���Ŀ���Ϊ�����ף�