题目内容
18．观察一列数，按某种规律在横线上填上适当的数：$\frac{1}{6}$，$\frac{1}{12}$，$\frac{1}{20}$，$\frac{1}{30}$，…，第99个数是$\frac{1}{10100}$．分析 观察数的规律可知，每一项都是分数，且分子为1，分母为该数的序号与比该数的序号多1的数的积，即第n个数为$\frac{1}{（n+1）（n+2）}$（n≥1）．
解答 解：第1个数：$\frac{1}{6}$=$\frac{1}{2×3}$；
第2个数：$\frac{1}{12}$=$\frac{1}{3×4}$；
第3个数：$\frac{1}{20}$=$\frac{1}{4×5}$，
…
第n个数：$\frac{1}{（n+1）（n+2）}$，
所以第99个数是：$\frac{1}{100×101}$=$\frac{1}{10100}$．
故答案是：$\frac{1}{10100}$．
点评 本题考查了数字的变化规律及有理数的加法运算．关键是找出分母中的数与序号的关系．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
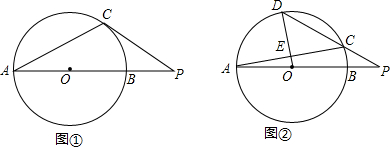
如图，PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于D、E，交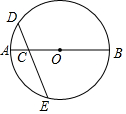
如图，C是⊙O的直径AB上一点，过点C作弦DE，使CD=CO，若$\widehat{AD}$的度数为35°，求$\widehat{BE}$的度数．