题目内容
哈市某社区为了打造美丽家乡哈尔滨形象,特购进菊花和太阳花共17100盆来搭配A、B两种园艺造型工100个摆放在社区,在购进的花中,菊花的盆数是太阳花盆数的
,
(1)求该社区购进的菊花和太阳花各多少盆?
(2)经过园艺设计可知:搭配一个A种园艺造型需要菊花100盆;搭配一个B种园艺造型需要菊花80盆,由于资金紧张,该社区需要考虑成本因素,经调查研究发现,搭配一个A种园艺造型的成本为600元,搭配一个B种园艺造型的成本为800元,则该社区最多搭配A种造型多少个时,才能使这100个园艺造型成本最低?
| 10 |
| 9 |
(1)求该社区购进的菊花和太阳花各多少盆?
(2)经过园艺设计可知:搭配一个A种园艺造型需要菊花100盆;搭配一个B种园艺造型需要菊花80盆,由于资金紧张,该社区需要考虑成本因素,经调查研究发现,搭配一个A种园艺造型的成本为600元,搭配一个B种园艺造型的成本为800元,则该社区最多搭配A种造型多少个时,才能使这100个园艺造型成本最低?
考点:一元一次不等式组的应用,二元一次方程组的应用
专题:
分析:(1)利用“9000盆菊花和8100盆太阳花”可列不等式组
,解不等式组可得解集;
(2)当x取值最大时,可使这100个园艺造型的成本最低.
|
(2)当x取值最大时,可使这100个园艺造型的成本最低.
解答:解:(1)∵购进菊花和太阳花共17100盆,菊花的盆数是太阳花盆数的
,
∴有9000盆菊花和8100盆太阳花
由题意得
,
解得47.5≤x≤50
(2)由于x是整数
所以x=48,49,50
即可搭配A种园艺造型48,49或50(个)
所以当搭配50个A种园艺,可使这100个园艺造型的成本最低.
| 10 |
| 9 |
∴有9000盆菊花和8100盆太阳花
由题意得
|
解得47.5≤x≤50
(2)由于x是整数
所以x=48,49,50
即可搭配A种园艺造型48,49或50(个)
所以当搭配50个A种园艺,可使这100个园艺造型的成本最低.
点评:本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某市为迎接大学生冬季运动会,正在进行城区人行道路翻新,准备只选用同一种正多边形地砖铺设地面.下列正多边形的地砖中,不能进行平面镶嵌的是( )
| A、正三角形 | B、正方形 |
| C、正六边形 | D、正八边形 |

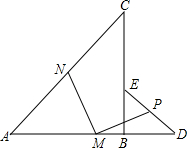 将等腰Rt△ABC和等腰Rt△BDE的直角顶点B重合,M、N、P分别是AD、AC、DE边的中点,且A、B、D在同一直线上,试说明MP与MN的关系.
将等腰Rt△ABC和等腰Rt△BDE的直角顶点B重合,M、N、P分别是AD、AC、DE边的中点,且A、B、D在同一直线上,试说明MP与MN的关系.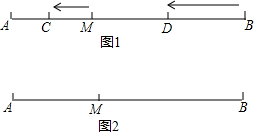 已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上).
已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上).