题目内容
5. 如图,△ABC中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:
如图,△ABC中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①△ABE≌△ACD;
②AO平分∠BAC;
③OB=OC;
④AO⊥BC;
⑤若AD=$\frac{1}{2}$BD,则OD=$\frac{1}{3}$OC;
其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据全等三角形的判定定理即可得到△ABE≌△ACD,故①正确;根据全等三角形的性质得到∠AEB=∠ADC,由平角的定义得到∠BDO=∠BEC,推出△BOD≌△COE,根据全等三角形的性质得到OD=OE,BO=OC,故③正确;推出△AOD≌△AOE,根据全等三角形的性质得到AO平分∠BAC,故②正确;根据等腰三角形的性质得到AO⊥BC,故④正确;过D作DF∥AO交BO于F,根据平行线分线段成比例定理得到OF=$\frac{1}{3}$OB,等量代换即可得到OD=$\frac{1}{3}$OC;故⑤正确.
解答 解:在△ABE与△ACD中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△ACD,故①正确;
∴∠AEB=∠ADC,
∴∠BDO=∠BEC,
∵AB=AC,AD=AE,
∴BD=CE,
在△BOD与△COE中,$\left\{\begin{array}{l}{∠BDO=∠CEO}\\{∠BOD=∠COE}\\{BD=CE}\end{array}\right.$,
∴△BOD≌△COE,
∴OD=OE,BO=OC,故③正确;
在△AOD与△AOE中,$\left\{\begin{array}{l}{AD=AE}\\{AO=AO}\\{OD=OE}\end{array}\right.$,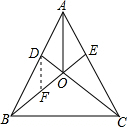
∴△AOD≌△AOE,
∴∠DAO=∠EAO,∠AOD=∠AOF,
∴AO平分∠BAC,故②正确;
∵AB=AC,AO平分∠BAC,
∴AO⊥BC,故④正确;
过D作DF∥AO交BO于F,
∵AD=$\frac{1}{2}$BD,
∴OF=$\frac{1}{3}$OB,
∵DF∥AO,
∴∠ODF=∠AOD,∠OFD=∠AOE,
∴∠ODF=∠OFD,
∴OD=OF,
∵OB=OC,
∴OD=$\frac{1}{3}$OC;故⑤正确;
故选D.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,平行线的性质,熟练掌握全等三角形的判定和性质是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | x2+5x+6=0 | B. | x2-5x+6=0 | C. | x2-5x-6=0 | D. | x2+5x-6=0 |
| A. | 有一组邻边相等的四边形是菱形 | |
| B. | 有一个角是直角的平行四边形是矩形 | |
| C. | 有一组对边平行的四边形是平行四边形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
| A. | m2•m4=m8 | B. | (-m3)2=m5 | C. | m0=1 | D. | (-m2)3=-m6 |
| A. | a>1 | B. | a<1 | C. | a≥1 | D. | a≤1 |
 如图,已知在长方形ABCD中,AB=10cm,BC=8cm,点E是CD中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E,若点P运动的时间为x秒,那么当x=4或6.6s时,△APE的面积等于32cm.
如图,已知在长方形ABCD中,AB=10cm,BC=8cm,点E是CD中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E,若点P运动的时间为x秒,那么当x=4或6.6s时,△APE的面积等于32cm. 如图,平行四边形ABCD,请你添一个条件∠A=90°,使四边形ABCD为矩形.
如图,平行四边形ABCD,请你添一个条件∠A=90°,使四边形ABCD为矩形. 如图,Rt△ABC在第一象限,∠BAC=90°,AB=AC=2,点A在直线y=x上,其中点A的横坐标为1,且AB∥x轴,AC∥y轴,若双曲线y=$\frac{k}{x}$(k≠0)与△ABC有交点,则k的取值范围是1≤k≤4.
如图,Rt△ABC在第一象限,∠BAC=90°,AB=AC=2,点A在直线y=x上,其中点A的横坐标为1,且AB∥x轴,AC∥y轴,若双曲线y=$\frac{k}{x}$(k≠0)与△ABC有交点,则k的取值范围是1≤k≤4.