题目内容
11.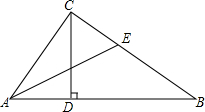 已知:如图,在△ABC中,∠C=90°
已知:如图,在△ABC中,∠C=90°(1)用直尺和圆规作△ABC的高CD、角平分线AE,CD、AE相交于点F;
(2)图中∠CEF、∠CFE相等吗?证明你的结论.
分析 (1)利用角平分线的作法以及高线作法得出即可;
(2)利用三角形外角的性质结合角平分线的性质得出即可.
解答  解:(1)如图所示:CD,AE即为所求;
解:(1)如图所示:CD,AE即为所求;
(2)∠CEF=∠CFE,
理由:∵△ABC中,∠C=90°,CD⊥AB于点D,
∴∠ACD+∠BCD=90°,∠DCB+∠B=90°,
∴∠ACD=∠B,
∵∠EAB+∠B=∠CEF,∠CAE+∠ACF=∠CFE,
由(1)得:∠CAE=∠EAB,
∴∠CEF=∠CFE.
点评 此题主要考查了复杂作图以及角平分线的性质和三角形外角的性质,正确利用三角形的外角的性质是解题关键.

练习册系列答案
相关题目
6.下面哪一个运算结果是相等的( )
| A. | ($\frac{2}{3}$)2与$\frac{{2}^{2}}{3}$ | B. | -22与(-2)2 | C. | -(-1)2011与(-1)2010 | D. | (-5)2与-52 |
20.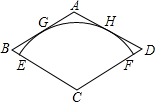 在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )
在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )
 在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )
在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | 1 |
1.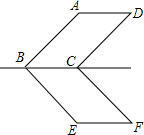 如图,?ABCD与?EBCF关于直线BC对称,若∠F=55°,则∠ABE的度数为( )
如图,?ABCD与?EBCF关于直线BC对称,若∠F=55°,则∠ABE的度数为( )
 如图,?ABCD与?EBCF关于直线BC对称,若∠F=55°,则∠ABE的度数为( )
如图,?ABCD与?EBCF关于直线BC对称,若∠F=55°,则∠ABE的度数为( )| A. | 55° | B. | 100° | C. | 110° | D. | 125° |
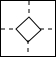
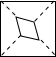
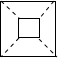
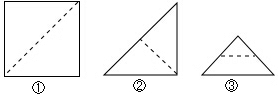 小麦拿了一张正方形纸(如图①),沿虚线对折一次得②,再对折一次得③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )
小麦拿了一张正方形纸(如图①),沿虚线对折一次得②,再对折一次得③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )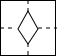
 如图,直线l:y=kx+b经过A(0,-1)、B(1,0)两点,则关于x的不等式kx+b>0的解集为x>1.
如图,直线l:y=kx+b经过A(0,-1)、B(1,0)两点,则关于x的不等式kx+b>0的解集为x>1. 如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.