题目内容
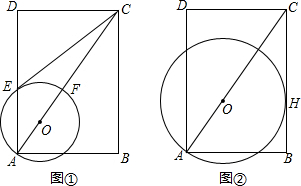
16. 如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.(1)求证:$\widehat{GE}=\widehat{EF}$;
(2)若$\widehat{BF}$的度数为70°,求∠C的度数.
分析 (1)要证明$\widehat{GE}$=$\widehat{EF}$,则要证明∠DAF=∠GAD,由题干条件能够证明之;
(2)根据$\widehat{BF}$的度数为70°,得到∠BAF=70°,于是得到∠B=∠AFB=$\frac{1}{2}$(180°-∠BAF)=55°,根据平行四边形的性质即可得到结论.
解答 (1)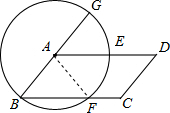 证明:连接AF.
证明:连接AF.
∵A为圆心,∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD为平行四边形,
∴AD∥BC,∠AFB=∠DAF,∠GAD=∠ABF,
∴∠DAF=∠GAD,
∴$\widehat{GE}$=$\widehat{EF}$;
(2)解:∵$\widehat{BF}$的度数为70°,
∴∠BAF=70°,
∵AB=AF,
∴∠B=∠AFB=$\frac{1}{2}$(180°-∠BAF)=55°,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠C=180°-∠B=125°.
点评 本题考查了平行四边形性质,平行线性质,圆周角定理等知识点的应用,关键是求出∠DAF=∠GAD,题目比较典型,难度不大.

练习册系列答案
相关题目
6. 如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )
 如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )| A. | 70° | B. | 100° | C. | 110° | D. | 12° |
7.将二次函数y=x2的图象先向右平移2个单位,再向上平移3个单位后,所得图象的函数表达式是( )
| A. | y=(x+2)2+3 | B. | y=(x-2)2-3 | C. | y=(x-2)2+3 | D. | y=(x+2)2-3 |
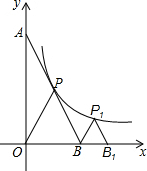 已知如图,Rt△AOB在直角坐标系中,∠BAO=30°,B点的坐标为(2,0),点P是斜边AB的中点,双曲线y=$\frac{k}{x}$在第一象限的图象过点P.
已知如图,Rt△AOB在直角坐标系中,∠BAO=30°,B点的坐标为(2,0),点P是斜边AB的中点,双曲线y=$\frac{k}{x}$在第一象限的图象过点P.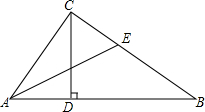 已知:如图,在△ABC中,∠C=90°
已知:如图,在△ABC中,∠C=90° 如图,已知∠AOB.
如图,已知∠AOB. 如图,线段AD,BC相交于点O,已知OA=4,OB=3,OC=9,OD=12,C,D,E三点在一直线上,求证:∠A+∠EDO=180°.
如图,线段AD,BC相交于点O,已知OA=4,OB=3,OC=9,OD=12,C,D,E三点在一直线上,求证:∠A+∠EDO=180°.